题目内容
6.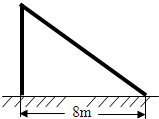 如图所示,台风过后,旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆在离地面6米处折断,请你求出旗杆原来的高度?
如图所示,台风过后,旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆在离地面6米处折断,请你求出旗杆原来的高度?
分析 直接利用勾股定理得出斜边长,进而得出答案.
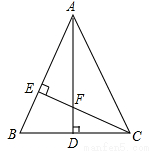
解答  解:如图所示:由题意可得,AB=6m,AC=8m,
解:如图所示:由题意可得,AB=6m,AC=8m,
在Rt△ABC中,
BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=10(m),
则6+10=16(m),
答:旗杆原来的高度为16m.
点评 此题主要考查了勾股定理的应用,正确构建直角三角形是解题关键.

练习册系列答案
相关题目
8.图象过点(0,0)且y随x的增大而减小的函数表达式为( )
| A. | y=x | B. | y=-x | C. | y=x+1 | D. | y=-x-1 |
1.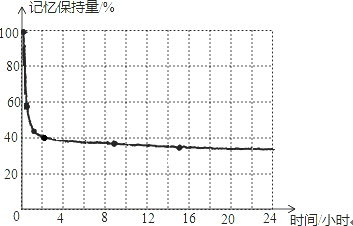 德国心理学家艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“记忆保持量是时间的函数”,他用无意义音节(由若干音节字母组成、能够读出、但无内容意义即不是词的音节)作记忆材料,用节省法计算保持和遗忘的数量.他通过测试,得到了一些数据如下表,然后又根据这些数据绘出了一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如下图.该曲线对人类记忆认知研究产生了重大影响.
德国心理学家艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“记忆保持量是时间的函数”,他用无意义音节(由若干音节字母组成、能够读出、但无内容意义即不是词的音节)作记忆材料,用节省法计算保持和遗忘的数量.他通过测试,得到了一些数据如下表,然后又根据这些数据绘出了一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如下图.该曲线对人类记忆认知研究产生了重大影响.
观察图象及表格,回答下列问题:
(1)2小时后,记忆保持量大约是多少?
(2)说明图中点A的坐标表示的实际意义.
(3)你从记忆遗忘曲线中还能获得什么信息?写出一条即可.
 德国心理学家艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“记忆保持量是时间的函数”,他用无意义音节(由若干音节字母组成、能够读出、但无内容意义即不是词的音节)作记忆材料,用节省法计算保持和遗忘的数量.他通过测试,得到了一些数据如下表,然后又根据这些数据绘出了一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如下图.该曲线对人类记忆认知研究产生了重大影响.
德国心理学家艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“记忆保持量是时间的函数”,他用无意义音节(由若干音节字母组成、能够读出、但无内容意义即不是词的音节)作记忆材料,用节省法计算保持和遗忘的数量.他通过测试,得到了一些数据如下表,然后又根据这些数据绘出了一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如下图.该曲线对人类记忆认知研究产生了重大影响.| 时间间隔 | 记忆保持量 |
| 刚记完 | 100% |
| 20分钟后 | 58.2% |
| 1小时后 | 44.2% |
| 8~9小时后 | 35.8% |
| 1天后 | 33.7% |
| 2天后 | 27.8% |
| 6天后 | 25.4% |
(1)2小时后,记忆保持量大约是多少?
(2)说明图中点A的坐标表示的实际意义.
(3)你从记忆遗忘曲线中还能获得什么信息?写出一条即可.
18.已知方程组$\left\{\begin{array}{l}{bx+ay=3}\\{ax-by=-1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,求a,b的值( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ |
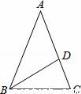
 如图,点O是△ABC内一点,连结OA、OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OA、OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.