题目内容
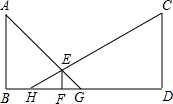 如图,路灯A、C的高度都为5m,路灯柱之间的距离BD为35m,身高1.5m的小明在线段BD上行走,试探究:小明在两个路灯下的影子长之和是否为定值?若为定值,则求出此定值;若不会定值,请说明理由.
如图,路灯A、C的高度都为5m,路灯柱之间的距离BD为35m,身高1.5m的小明在线段BD上行走,试探究:小明在两个路灯下的影子长之和是否为定值?若为定值,则求出此定值;若不会定值,请说明理由.考点:相似三角形的应用
专题:
分析:根据题意利用相似三角形的性质得到比例式,进行等量代换,利用等比性质可得相关数值.
解答:解:小明在两个路灯下的影子长之和为定值,
理由:∵AB∥EF∥DC,
∴△ABG∽△EFG,△EFH∽△CDH,
∴
=
,
=
,
∴
=
,
=
,
∴
=
=
,
设FG+FH=x,则
=
,
解得:x=15,
故此定值为15.
理由:∵AB∥EF∥DC,
∴△ABG∽△EFG,△EFH∽△CDH,
∴
| EF |
| AB |
| FG |
| BG |
| EF |
| CD |
| HF |
| HD |
∴
| 1.5 |
| 5 |
| FG |
| BF+FG |
| 1.5 |
| 5 |
| FH |
| HF+DF |
∴
| 1.5+1.5 |
| 5+5 |
| FG+FH |
| 35+FH+FG |
| 3 |
| 10 |
设FG+FH=x,则
| x |
| 35+x |
| 3 |
| 10 |
解得:x=15,
故此定值为15.
点评:此题主要考查了相似三角形的应用;用到的知识点为:平行于三角形一边的直线与三角形另两边相交,截得的两三角形相似;得出相似三角形的对应边成比例关系是解决本题的突破点.

练习册系列答案
相关题目
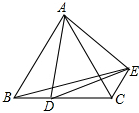 如图,在等边三角ABC中,AB=6,D是BC上一点,且BC等于3BD,△ABD绕点A旋转后得到△ACE,则BE长度为( )
如图,在等边三角ABC中,AB=6,D是BC上一点,且BC等于3BD,△ABD绕点A旋转后得到△ACE,则BE长度为( )A、2
| ||
B、
| ||
C、4
| ||
| D、7 |
 用一个小立方块搭一个几何体,它的主视图和俯视图如图所示,尝试画出所有可能的左视图,想一想,搭成这个几何体最少需要多少个小立方块?最多需要多少个小立方块?
用一个小立方块搭一个几何体,它的主视图和俯视图如图所示,尝试画出所有可能的左视图,想一想,搭成这个几何体最少需要多少个小立方块?最多需要多少个小立方块? 在Rt△ABC中,∠C=90°,点D、E分别为BC、AC上的点.那么AD2+BE2与DE2+AB2的大小有什么关系?请说明理由.
在Rt△ABC中,∠C=90°,点D、E分别为BC、AC上的点.那么AD2+BE2与DE2+AB2的大小有什么关系?请说明理由.