题目内容
 在Rt△ABC中,∠C=90°,点D、E分别为BC、AC上的点.那么AD2+BE2与DE2+AB2的大小有什么关系?请说明理由.
在Rt△ABC中,∠C=90°,点D、E分别为BC、AC上的点.那么AD2+BE2与DE2+AB2的大小有什么关系?请说明理由.考点:勾股定理
专题:
分析:直接根据勾股定理进行解答即可.
解答:解:AD2+BE2=DE2+AB2.
理由:∵在Rt△ABC中,∠C=90°,
∴AB2=AC2+BC2①,DE2=CE2+CD2②,AD2=AC2+CD2③,BE2=CE2+BC2④,
∴①+②得,AB2+DE2=AC2+BC2+CE2+CD2,
③+④得,AD2+BE2=AC2+CD2+CE2+BC2,
∴AD2+BE2=DE2+AB2.
理由:∵在Rt△ABC中,∠C=90°,
∴AB2=AC2+BC2①,DE2=CE2+CD2②,AD2=AC2+CD2③,BE2=CE2+BC2④,
∴①+②得,AB2+DE2=AC2+BC2+CE2+CD2,
③+④得,AD2+BE2=AC2+CD2+CE2+BC2,
∴AD2+BE2=DE2+AB2.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
若多项式2x2+3y的值是1,那么多项式4x2+6y-2的值是( )
| A、0 | B、1 | C、2 | D、3 |
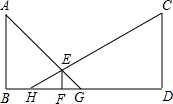 如图,路灯A、C的高度都为5m,路灯柱之间的距离BD为35m,身高1.5m的小明在线段BD上行走,试探究:小明在两个路灯下的影子长之和是否为定值?若为定值,则求出此定值;若不会定值,请说明理由.
如图,路灯A、C的高度都为5m,路灯柱之间的距离BD为35m,身高1.5m的小明在线段BD上行走,试探究:小明在两个路灯下的影子长之和是否为定值?若为定值,则求出此定值;若不会定值,请说明理由.