��Ŀ����
��֪����y=2x2+4x-3.
(1)ͨ���䷽,д�������ߵĿ��ڷ��Գ���Ͷ�������;
(2)�ֱ������������x�ᡢy��Ľ�������.
(1) �Գ�����ֱ��x=-1,��������Ϊ(-1,-5);(2) ��������Ϊ(0,-3). �������������������1�����ݵ�ֵ��ֱ�ӵõ����κ����Ŀ��ڷ��Ѷ��κ������ɶ���ʽ����д���������ꡢ�Գ�� ��2������κ����������Ӧ�ĵ�ֵ���ɵõ����κ���ͼ������Ľ������ꣻ����κ����������Ӧ�ĵ�ֵ���ɵõ����κ���ͼ������Ľ������ꣻ ��������� (1)y=2x2+4x-3=2(...
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ


 ��
�� 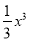 ��
�� 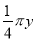 ��
�� 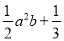 �У�����ʽ�ĸ����У�������
�У�����ʽ�ĸ����У�������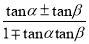
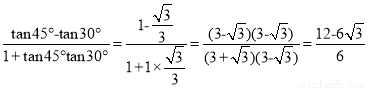 =2-
=2-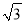 .
.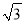 ��1.732,
��1.732, 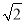 ��1.414)
��1.414)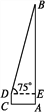
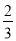 ]=0��[3.14]=3�����˹涨[
]=0��[3.14]=3�����˹涨[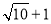 ]��ֵΪ_____��
]��ֵΪ_____��