题目内容
3. 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
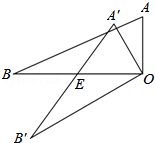
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.A.如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$;
B.用科学计算器计算:${13^5}×\sqrt{13}sin{13°}≈$301145.6.(精确到0.1)
分析 A、作辅助线.构建直角△EMO,设EM=a,利用三角函数表示OM的长,再利用勾股定理列方程,求出a的值,则B′E=3$\sqrt{5}$-2a代入计算;
B、利用计算器计算.
解答  解:A.过O作OM⊥A′B′,垂足为M,
解:A.过O作OM⊥A′B′,垂足为M,
∵A′O=OE=3,
∴A′M=EM,
由勾股定理得:A′B′=AB=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
设EM=a,则B′M=3$\sqrt{5}$-a,
在Rt△B′MO中,tan∠MB′O=$\frac{OM}{B′M}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴OM=$\frac{3\sqrt{5}-a}{2}$,
由勾股定理得:a2+$(\frac{3\sqrt{5}-a}{2})^{2}$=32,
5a2-6$\sqrt{5}$a+9=0,
a1=a2=$\frac{3\sqrt{5}}{5}$,
∴B′E=3$\sqrt{5}$-2a=3$\sqrt{5}$-$\frac{6\sqrt{5}}{5}$=$\frac{9\sqrt{5}}{5}$;
B.135×$\sqrt{13}$sin13°≈301145.6;
故答案为:A、$\frac{9\sqrt{5}}{5}$;B、301145.6.
点评 本题考查了旋转的性质和使用计算器计算,明确旋转前后的边和角相等,利用等腰三角形三线合一的性质及三角函数表示各边的长,在不同的直角三角形中,同角的三角函数值相等这一结论要熟练掌握.

练习册系列答案
相关题目
14.如图中,∠1与∠2是内错角的是( )
| A. |  | B. |  | C. |  | D. |  |
11.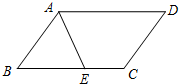 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )
 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E.则线段BE、EC的长度分别为( )| A. | 2和3 | B. | 3和2 | C. | 4和1 | D. | 1和4 |
12.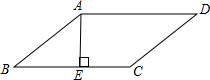 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
 如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )
如图,在?ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则?ABCD的周长为( )| A. | 4+2$\sqrt{2}$ | B. | 12+6$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 2+$\sqrt{2}$或12+6$\sqrt{2}$ |
13.若代数式$\frac{\sqrt{x+1}}{(x+3)^{2}}$有意义,则实数x的取值范围是( )
| A. | x≥-1且x≠-3 | B. | x≥-1 | C. | x>-1 | D. | x>-1且x≠3 |
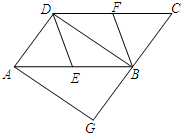 如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB,交CB的延长线于点G,∠G=90°.
如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB,交CB的延长线于点G,∠G=90°. 如图,在?ABCD中,AC、BD相交于点O,AC=10,BD=8,CD=6,求△OAB的周长.
如图,在?ABCD中,AC、BD相交于点O,AC=10,BD=8,CD=6,求△OAB的周长. 如图,?ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,?ABCD满足矩形条件时,能判断四边形CODE是菱形.
如图,?ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,?ABCD满足矩形条件时,能判断四边形CODE是菱形.