题目内容
2.不等式组$\left\{\begin{array}{l}{2x>-1}\\{-3x+9≥0}\end{array}\right.$所有整数解的和是6.分析 先求出不等式组的解集,再求出不等式组的整数解,最后求出答案即可.
解答 解:解不等式2x>-1,得x>-$\frac{1}{2}$,
解不等式-3x+9≥0,得x≤3,
所以不等式组$\left\{\begin{array}{l}{2x>-1}\\{-3x+9≥0}\end{array}\right.$的解集为-$\frac{1}{2}$<x≤3,
则不等式组的整数解为0,1,2,3,
0+1+2+3=6.
故答案为6.
点评 本题考查了解一元一次不等式组,求不等式组的整数解的应用,解此题的关键是求出不等式组的解集,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列事件是必然事件的是( )
| A. | 打开电视机,它正在播放动画片 | |
| B. | 播下一颗种子,种子一定会发芽 | |
| C. | 买100张中奖率为1%的彩票一定会中奖 | |
| D. | 太阳从东方升起 |
7.在Rt△ABC中,其中两边的长恰好是方程x2-14x+48=0的两个根,则这个直角三角形的斜边长是( )
| A. | 10 | B. | 48 | C. | 36 | D. | 10或8 |
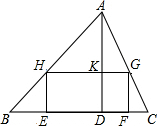 如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.
如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.