题目内容
12.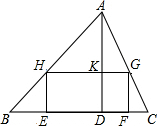 如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.
如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.
分析 设EF=4k,EH=3k,则AK=12-3k,先证明△AHG∽△ABC,然后由相似三角形的性质可知$\frac{GH}{BC}=\frac{AK}{AD}$,即$\frac{4k}{24}=\frac{12-3k}{12}$从而可求得k=2.4,然后可求得EF和EH的长,最后求得四边形EFGH的面积.
解答 解:设EF=4k,EH=3k,则AK=12-3k.
∵HG∥BC,
∴△AHG∽△ABC.
∴$\frac{GH}{BC}=\frac{AK}{AD}$,即$\frac{4k}{24}=\frac{12-3k}{12}$.
解得:k=2.4cm.
∴EF=4×2.4=9.6cm,HE=2.4×3=7.2cm.
∴四边形EFGH的面积=EF•EH=9.6×7.2=69.12cm2.
点评 本题主要考查的是相似三角形的性质和判定,明确相似三角形的对应高的比等于相似比是解题的关键.

练习册系列答案
相关题目
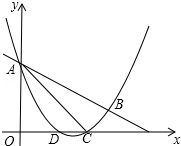 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0). 如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C. 如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.
如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC. 如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°. 如图所示,A为反比例函数$y=\frac{k}{x}$图象上一点,AB垂直x轴,垂足为B点,若S△AOB=3,则k的值为6.
如图所示,A为反比例函数$y=\frac{k}{x}$图象上一点,AB垂直x轴,垂足为B点,若S△AOB=3,则k的值为6.