题目内容
7.在Rt△ABC中,其中两边的长恰好是方程x2-14x+48=0的两个根,则这个直角三角形的斜边长是( )| A. | 10 | B. | 48 | C. | 36 | D. | 10或8 |
分析 解方程x2-14x+48=0求出直角三角形的两边是6,8,这两边可能是两条直角边,根据勾股定理即可求得斜边,也可能是一条直角边和一条斜边,则斜边一定是8.
解答 解:∵直角三角形的两边长恰好是方程x2-14x+48=0的两个根,
∴直角三角形的两边是6,8,
当是原方程的两边的是两条直角边时,根据勾股定理得其斜边为$\sqrt{{6}^{2}+{8}^{2}}$=10;
当是原方程的两边的是一条直角边,和斜边时,斜边一定是,8.
故选D.
点评 本题主要考了一元二次方程根与系数的关系,查勾股定理,即斜边的平方等于两直角边的平方和及解一元二次方程.注意到分两种情况进行讨论是解决本题的关键.

练习册系列答案
相关题目
 如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.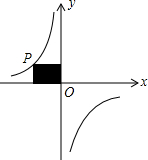 如图,P是反比例函数y=$\frac{k}{x}$的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是-6.
如图,P是反比例函数y=$\frac{k}{x}$的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是-6. 如图:线段AB=20cm,点C是线段AB上一点,点M是线段BC的中点,点N是线段AB的中点且BM=4cm,求线段NC的长.
如图:线段AB=20cm,点C是线段AB上一点,点M是线段BC的中点,点N是线段AB的中点且BM=4cm,求线段NC的长.