题目内容
6.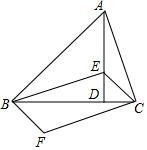 如图,在△ABC中,AD⊥BC于点D,∠ABD=45°,在AD上取一点E,连接BE,使得BE=AC,连接CE,将线段CA绕点C逆时针旋转90°,到达CF的位置,连接BF.已知∠CAD=∠BCF.
如图,在△ABC中,AD⊥BC于点D,∠ABD=45°,在AD上取一点E,连接BE,使得BE=AC,连接CE,将线段CA绕点C逆时针旋转90°,到达CF的位置,连接BF.已知∠CAD=∠BCF.(1)试判断DE与CD之间的数量关系,并说明理由;
(2)求证:四边形BFCE是平行四边形;
(3)若BC=7,DE=2,求线段CA旋转过程中扫过的面积.
分析 (1)根据HL证明Rt△BDE≌Rt△ADC可得结论;
(2)证明BE=CF和BE∥CF,由一组对边平行且相等的四边形是平行四边形可得结论;
(3)由图形可知:线段CA旋转过程中扫过的面积是以AC为半径,圆心角为90度的扇形的面积,求出AC的长,代入公式即可.
解答 解:(1)DE=CD;
理由是:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ABD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE=AC,
∴Rt△BDE≌Rt△ADC(HL),
∴DE=CD;
(2)由旋转得:AC=CF,
∵BE=AC,
∴BE=CF,
由(1)得Rt△BDE≌Rt△ADC,
∴∠DBE=∠DAC,
∵∠DAC=∠BCF,
∴∠DBE=∠BCF,
∴BE∥FC,
∴四边形BFCE是平行四边形;
(3)由(1)得DE=DC=2,
∵BC=7,
∴AD=BD=7-2=5,
在Rt△ADC中,由勾股定理得:AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$,
∴S=$\frac{90π×(\sqrt{29})^{2}}{360}$=$\frac{29}{4}$π,
则线段CA旋转过程中扫过的面积为$\frac{29}{4}$π.
点评 本题是四边形的综合题,难度适中,考查了直角三角形全等的性质和判定、等腰直角三角形的性质和判定、勾股定理、扇形面积公式、平行四边形的性质和判定,熟练掌握直角三角形全等和平行四边形的判定是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
11.要了解某市九年级学生的视力状况,从中抽查了500名学生的视力状况,那么样本是指( )
| A. | 某市所有的九年级学生 | B. | 某市所有的九年级学生的视力状 | ||
| C. | 被抽查的500名九年级学生 | D. | 被抽查的500名学生的视力状况 |
15.2sin45°的值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{2}$ | D. | 3 |
 如图,l1∥l2,∠1=35°15′,则∠2的度数为144°45'.
如图,l1∥l2,∠1=35°15′,则∠2的度数为144°45'. 如图:在平行四边形ABCD中,∠DAB的平分线AE交CD于点E,BC=9,AB=15,则CE=6.
如图:在平行四边形ABCD中,∠DAB的平分线AE交CD于点E,BC=9,AB=15,则CE=6.
 填空:
填空: