题目内容
16. 如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)| A. | 30(3+$\sqrt{3}$)米 | B. | 45(2+$\sqrt{3}$)米 | C. | 30(1+3$\sqrt{3}$)米 | D. | 45(1+$\sqrt{2}$)米 |
分析 作AE⊥CD于点E,则△AED和△ABD都是等腰直角三角形,即可求得DE的长,然后在直角三角形中利用三角函数求得CE的长,进而求得CD的长.
解答  解:作AE⊥CD于点E.
解:作AE⊥CD于点E.
在直角△ABD中,∠ADB=45°,
∴DE=AE=BD=AB=90(米),
在直角△AEC中,CE=AE•tan∠CAE=90×$\frac{\sqrt{3}}{3}$=30$\sqrt{3}$(米).
则CD=(90+30$\sqrt{3}$)米.
故选A.
点评 本题考查解直角三角形的应用-仰角俯角问题的应用,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
4.下列四条线段成比例的是( )
| A. | a=2,b=$\sqrt{5}$,c=2$\sqrt{3}$,d=$\sqrt{3}$ | B. | a=$\sqrt{2}$,b=2,c=1,d=$\sqrt{2}$ | ||
| C. | a=4,b=6,c=5,d=10 | D. | a=12,b=8,c=15,d=11 |
5.下列命题中,错误的是( )
| A. | 如果k=0,则k$\overrightarrow{a}$=0 | B. | 如果m,n为实数,则m(n$\overrightarrow{a}$)=(mn)$\overrightarrow{a}$ | ||
| C. | 如果m,n为实数,则(m+n)$\overrightarrow{a}$=m$\overrightarrow{a}$+n$\overrightarrow{a}$ | D. | 如果m为实数,则m($\overrightarrow{a}+\overrightarrow{b}$)=m$\overrightarrow{a}$+n$\overrightarrow{b}$ |
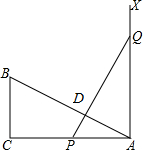 如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.
如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.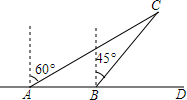 如图,上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A、B两处分别测得小岛C在北偏东60°和北偏东45°方向上,已知小岛C周围方圆30海里的海域内有暗礁.该船若继续向东方向航行,有触礁的危险吗?并说明理由.
如图,上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A、B两处分别测得小岛C在北偏东60°和北偏东45°方向上,已知小岛C周围方圆30海里的海域内有暗礁.该船若继续向东方向航行,有触礁的危险吗?并说明理由.