题目内容
6.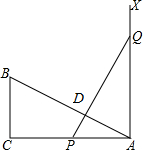 如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.
如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.
分析 根据三角形全等的性质得出∠BAC=∠APQ,进而得出∠PQA=∠DAQ,从而求出AD=PD=QD,则AD=$\frac{1}{2}$PQ=$\frac{1}{2}$AB=4.
解答 解:∵△ABC≌△PQA,PQ=AB.
∴∠BAC=∠APQ,
∴PD=DA,
∵∠BAC+∠BAQ=90°,∠APQ+∠AQP=90°,
∴∠PQA=∠DAQ,
∴AD=DQ,
∴AD=PD=QD,
∴AD=$\frac{1}{2}$PQ,
∵PQ=AB=8,
∴PQ=4.
故答案为4.
点评 本题考查了三角形全等的性质,等腰三角形的判定和性质,熟练掌握三角形全等的性质是解题的关键.

练习册系列答案
相关题目
17.$\sqrt{144}$的平方根是( )
| A. | ±12 | B. | 12 | C. | ±$\sqrt{12}$ | D. | $\sqrt{12}$ |
1.用配方法解方程x2+6x+4=0,下列变形正确的是( )
| A. | (x+3)2=-4 | B. | (x-3)2=4 | C. | (x+3)2=5 | D. | (x+3)2=±$\sqrt{5}$ |
18.抛物线y=-3x2+1的对称轴是( )
| A. | 直线x=$\frac{1}{3}$ | B. | 直线x=-$\frac{1}{3}$ | C. | y轴 | D. | 直线x=3 |
15.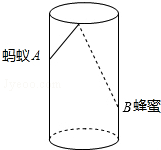 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )| A. | 13cm | B. | $\sqrt{61}$cm | C. | 2$\sqrt{61}$cm | D. | 20cm |
16. 如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
 如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)| A. | 30(3+$\sqrt{3}$)米 | B. | 45(2+$\sqrt{3}$)米 | C. | 30(1+3$\sqrt{3}$)米 | D. | 45(1+$\sqrt{2}$)米 |
 如图,正方形B的面积是144.
如图,正方形B的面积是144.