题目内容
5.下列命题中,错误的是( )| A. | 如果k=0,则k$\overrightarrow{a}$=0 | B. | 如果m,n为实数,则m(n$\overrightarrow{a}$)=(mn)$\overrightarrow{a}$ | ||
| C. | 如果m,n为实数,则(m+n)$\overrightarrow{a}$=m$\overrightarrow{a}$+n$\overrightarrow{a}$ | D. | 如果m为实数,则m($\overrightarrow{a}+\overrightarrow{b}$)=m$\overrightarrow{a}$+n$\overrightarrow{b}$ |
分析 根据向量的运算法则求解即可求得答案,注意掌握排除法在选择题中的应用.
解答 解:A、如果k=0,则k$\overrightarrow{a}$=$\overrightarrow{0}$,故本选项错误;
B、如果m,n为实数,则m(n$\overrightarrow{a}$)=(mn)$\overrightarrow{a}$;故本选项正确;
C、如果m,n为实数,则(m+1n)$\overrightarrow{a}$=m$\overrightarrow{a}$+n$\overrightarrow{a}$;故本选项正确;
D、如果m为实数,则m($\overrightarrow{a}+\overrightarrow{b}$)=m$\overrightarrow{a}$+n$\overrightarrow{b}$;故本选项正确.
故选A.
点评 此题考查了平面向量的运算法则.注意掌握分配律,交换律的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.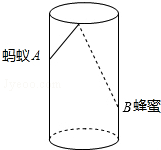 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )| A. | 13cm | B. | $\sqrt{61}$cm | C. | 2$\sqrt{61}$cm | D. | 20cm |
16. 如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
 如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)
如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是( )(结果可以保留根号)| A. | 30(3+$\sqrt{3}$)米 | B. | 45(2+$\sqrt{3}$)米 | C. | 30(1+3$\sqrt{3}$)米 | D. | 45(1+$\sqrt{2}$)米 |
10.下列各题运算正确的是( )
| A. | 3x+3y=6xy | B. | x+x=x2 | C. | 16y2-9y2=7 | D. | 9a2b-9ba2=0 |
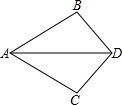 如图,已知AB=AC,请你添加一个条件:BD=CD,使△ABD≌△ACD.
如图,已知AB=AC,请你添加一个条件:BD=CD,使△ABD≌△ACD.