Question

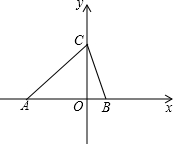在直角坐标系中，已知点A、B的坐标是（a，0）（b，0），a，b满足方程组

2a+b=-5 3a-2b=-11

，c为y轴正半轴上一点，且S_△ABC=6．
（1）求A、B、C三点的坐标；
（2）是否存在点P（t，t），使S_△PAB=

1

3

S_△ABC？若存在，请求出P点坐标；若不存在，请说明理由；
（3）若M是AC的中点，N是BC上一点，CN=2BN，连AN、BM相交于点D，求四边形CMDN的面积是

 

．

Answer 1

考点：坐标与图形性质,解二元一次方程组,三角形的面积

专题：

分析：（1）解出方程组即可得到时点A，B的坐标，利用S_△ABC=6，求出点C的坐标．
（2）利用S_△PAB=

1

3

S_△ABC求出点P的坐标．
（3）先求出点M，N的坐标，再求出BM所在的直线，AN所在的直线，进而求出点D的坐标，利用三角形面积公式可求出S_△ADB，S_△ABN及S_△BND，利用四边形CMDN的面积=△CBM的面积-△BND的面积求出四边形CMDN的面积．

解答：解：（1）方程组

2a+b=-5 3a-2b=-11

，解得

a=-3 6=1

，
∴A（-3，0），B（1，0），
∵c为y轴正半轴上一点，且S_△ABC=6，
∴

1

2

AB•OC=6，解得OC=3
∴C（0，3）
（2）∵P（t，t），且S_△PAB=

1

3

S_△ABC，
∴

1

2

×4×|t|=

1

3

×6，解得t=±1，
∴P（1，1）或（-1，-1）
（3）如图，

∵M是AC的中点，CN=2BN，
∴点M的坐标为：（-

3

2

，

3

2

），点N的坐标为（

2

3

，1）
设BM所在的直线为y=k₁x+b₁，AN所在的直线为y=k₂x+b₂
∵A（-3，0），B（1，0），
方程组为

3 2 =- 3 2 k1+b1 0=k1+b1

，

1= 2 3 k2+b2 0=-3k2+b2

解得

k1=- 3 5 b1= 3 5

，

k2= 3 11 b2= 9 11

∴BM所在的直线为y=-

3

5

x+

3

5

，AN所在的直线为y=

3

11

x+

9

11

．

y=- 3 5 x+ 3 5 y= 3 11 x+ 9 11

解得

x=- 1 4 y= 3 4

∴点D的坐标为（-

1

4

，

3

4

），
∴S_△ADB=

1

2

×4×

3

4

=

3

2

，
∵S_△ABN=

1

3

S_△ABC=6×

1

3

=1=2，
∴S_△BND=2-

3

2

=

1

2

，
∴四边形CMDN的面积=△CBM的面积-△BND的面积=

1

2

×6-

1

2

=

5

2

．
故答案为：

5

2

．

点评：本题主要考查了坐标与图形性质，三角形的面积和解二元一次方程组，解题的关键是求出点D的坐标．