题目内容
已知直线l1:y=kx+b经过点A(-1,-6),且与直线l2:y=ax+3相交于点B(2,a).
(1)求直线l1和直线l2对应函数的表达式;
(2)求直线l1、l2及x轴所围成的三角形的面积.
(1)求直线l1和直线l2对应函数的表达式;
(2)求直线l1、l2及x轴所围成的三角形的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)先直线l2:y=ax+3相交于点B(2,a)求得B点的坐标,然后根据待定系数法即可求得.
(2)先求得直线l1:y=x-5与x轴交点坐标,直线l2:y=-3x+3与x轴交点坐标,然后根据这两点和C点即可计算出△ABC的面积.
(2)先求得直线l1:y=x-5与x轴交点坐标,直线l2:y=-3x+3与x轴交点坐标,然后根据这两点和C点即可计算出△ABC的面积.
解答:解:(1)∵点B(2,a)在直线l2:y=ax+3上.
∴a=2a+3,则a=-3,
故直线l2对应函数的表达式为y=-3x+3.
又直线l1:y=kx+b经过点A(-1,-6)和B(2,-3),
则
解这个方程组,得
故直线l1对应函数的表达式为y=x一5.
(2)直线l1:y=x-5与x轴交点坐标是(5,0),
直线l2:y=-3x+3与x轴交点坐标是(1,0),
又∵点B的坐标是(2,-3).
∴所求的面积S=
×(5-1)×|-3|=6.
∴a=2a+3,则a=-3,
故直线l2对应函数的表达式为y=-3x+3.
又直线l1:y=kx+b经过点A(-1,-6)和B(2,-3),
则
|
解这个方程组,得
|
故直线l1对应函数的表达式为y=x一5.
(2)直线l1:y=x-5与x轴交点坐标是(5,0),
直线l2:y=-3x+3与x轴交点坐标是(1,0),
又∵点B的坐标是(2,-3).
∴所求的面积S=
| 1 |
| 2 |
点评:本题考查了两直线的相交问题,用待定系数法确定函数的解析式,是常用的一种解题方法.

练习册系列答案
相关题目
已知下列命题:①若a>0,b>0,则a+b>0;②若a≠b,则a2≠b2;③两点之间,线段最短;④同位角相等,两直线平行;⑤若2a-3和a+3是非负数m的平方根,则m=9.其中真命题的个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知:
是二次根式,则字母x应满足条件是( )
|
| A、x为正数 | B、x为非负数 |
| C、x>3 | D、x>-3 |
 如图,是由7个大小相同的正方体组成的几何体,该几何体的主视图是( )
如图,是由7个大小相同的正方体组成的几何体,该几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
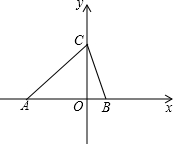 在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组
在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组 解不等式组
解不等式组