题目内容
已知直线a∥b,直线c分别与直线a,b相交于点E,F,点A,B分别在直线a,b上,且在直线c的左侧,点P是直线c上一动点(不与点E,F重合),设∠PAE=∠1,∠APB=∠2,∠PBF=∠3.

(1)如图,当点P在线段EF上运动时,试探索∠1,∠2,∠3之间的关系,并给出证明;
(2)当点P在线段EF外运动时,画出图形,(1)中的结论是否还成立?若成立,给出证明;若不成立,请你探索∠1,∠2,∠3之间的关系(不需要证明).

(1)如图,当点P在线段EF上运动时,试探索∠1,∠2,∠3之间的关系,并给出证明;
(2)当点P在线段EF外运动时,画出图形,(1)中的结论是否还成立?若成立,给出证明;若不成立,请你探索∠1,∠2,∠3之间的关系(不需要证明).
考点:平行线的性质
专题:
分析:(1)过点P作直线PM,使PM∥直线a,根据两直线平行,内错角相等即可求解;
(2)分当点P在FE的延长线上运动时和当点P在EF的延长线上运动时两种情况进行讨论即可.
(2)分当点P在FE的延长线上运动时和当点P在EF的延长线上运动时两种情况进行讨论即可.
解答: 解:(1)∠1+∠3=∠2.
解:(1)∠1+∠3=∠2.
证明:过点P作直线PM,使PM∥直线a.
则∠1=∠APM,
∵a∥b,PM∥a,
∴PM∥b.
则∠3=∠MPB.
∴∠1+∠3=∠APM+∠MPB=∠APB.
即∠1+∠3=∠2.
(2)(1)中的结论不成立.
有两种情况.
①当点P在FE的延长线上运动时,(如备用图①),有:∠1+∠2=∠3.
②当点P在EF的延长线上运动时(如备用图②),有∠2+∠3=∠1.
 解:(1)∠1+∠3=∠2.
解:(1)∠1+∠3=∠2.证明:过点P作直线PM,使PM∥直线a.
则∠1=∠APM,
∵a∥b,PM∥a,
∴PM∥b.
则∠3=∠MPB.
∴∠1+∠3=∠APM+∠MPB=∠APB.
即∠1+∠3=∠2.
(2)(1)中的结论不成立.
有两种情况.
①当点P在FE的延长线上运动时,(如备用图①),有:∠1+∠2=∠3.
②当点P在EF的延长线上运动时(如备用图②),有∠2+∠3=∠1.
点评:本题重点考查了平行线的性质:两直线平行,内错角相等,正确作出辅助线是关键.

练习册系列答案
相关题目
圆锥的底面半径为2,母线长为4,则它的全面积为( )
| A、8π | ||
| B、12π | ||
C、4
| ||
| D、4π |
 如图,是由7个大小相同的正方体组成的几何体,该几何体的主视图是( )
如图,是由7个大小相同的正方体组成的几何体,该几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
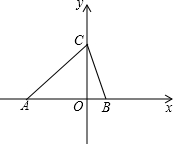 在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组
在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组 解不等式组
解不等式组 某学校wie丰富课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成直方图,如图.
某学校wie丰富课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成直方图,如图.