题目内容
已知等腰三角形的两边长是a，b，满足|a-b+2|+（2a+3b-11）2=0，则此等腰三角形的周长是（ ）
| A、5 | B、6 | C、7 | D、5或7 |
考点：等腰三角形的性质,解二元一次方程组,三角形三边关系
专题：
分析：先根据非负数的性质列式求出a、b的值，再分a的值是腰长与底边两种情况讨论求解．
解答：解：∵|a-b+2|+（2a+3b-11）2=0，
∴
，
解得
，
①1是腰长时，三角形的三边分别为1、1、3，
不能组成三角形；
②1是底边时，三角形的三边分别为1、3、3，
能组成三角形，周长=1+3+3=7，
所以，三角形的周长为7．
故选C．
∴
|
解得
|
①1是腰长时，三角形的三边分别为1、1、3，
不能组成三角形；
②1是底边时，三角形的三边分别为1、3、3，
能组成三角形，周长=1+3+3=7，
所以，三角形的周长为7．
故选C．
点评：本题考查了等腰三角形的性质，绝对值与平方的非负性，根据几个非负数的和等于0，则每一个算式都等于0求出a、b的值是解题的关键，难点在于要分情况讨论并且利用三角形的三边关系进行判断．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
圆锥的底面半径为2，母线长为4，则它的全面积为（ ）
| A、8π | ||
| B、12π | ||
C、4
| ||
| D、4π |
某次知识竞赛共20道题，每一题答对得10分，答错或不答都扣5分，小英得分不低于90分．设她答对了x道题，则根据题意可列出不等式为（ ）
| A、10x-5（20-x）≥90 |
| B、10x-5（20-x）＞90 |
| C、10x-（20-x）≥90 |
| D、10x-（20-x）＞90 |
已知：
是二次根式，则字母x应满足条件是（ ）
|
| A、x为正数 | B、x为非负数 |
| C、x＞3 | D、x＞-3 |
A，B两点在一次函数图象上的位置如图，两点的坐标分别为A（x，y），B（x-a，y-b），下列结论正确的是（ ）| A、a＞0，b＞0 |
| B、a＞0，b＞0 |
| C、a＜0，b＜0 |
| D、a＜0，b＞0 |
如图，是由7个大小相同的正方体组成的几何体，该几何体的主视图是（ ）A、 |
B、 |
C、 |
D、 |
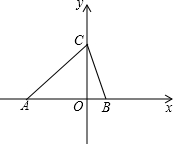在直角坐标系中，已知点A、B的坐标是（a，0）（b，0），a，b满足方程组
某学校wie丰富课间自由活动的内容，随机选取本校100名学生进行调查，调查内容是“你最喜欢的自由活动项目是什么”，整理收集到的数据，绘制成直方图，如图．