题目内容
10. (1)如图,点C在线段AB上,点M,N分别是线段AC,BC的中点.
(1)如图,点C在线段AB上,点M,N分别是线段AC,BC的中点.①若AC=8cm,CB=6cm,求线段MN的长;
②若AC+CB=a cm,直接写出线段MN=$\frac{1}{2}$acm.
(2)若C在线段AB的延长线上,且满足AC-BC=bcm,M,N分别为线段AC,BC的中点,直接写出线段MN=$\frac{1}{2}$bcm.
分析 (1)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(3)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案.
解答 解:(1)①∵点M,N分别是线段AC,BC的中点,
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$CB,
∵AC=8 cm,CB=6 cm,
∴MC=4 cm,CN=3 cm,
∴MN=7 cm;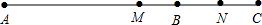
②MN=CM+CN=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$a;
故答案为:$\frac{1}{2}$a;
(2)MN=$\frac{b}{2}$,理由如下:如图:
由M、N分别是AC、BC的中点,
得MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC.
由线段的和差,得MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$bcm;
故答案为:$\frac{1}{2}$b.
点评 本题考查了两点间的距离,利用了线段中点的性质,线段的和差.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.若2amb3与-3a4bn是同类项,则m,n的值分别为( )
| A. | 2,1 | B. | 3,4 | C. | 3,2 | D. | 4,3 |
5.下列方程变形中,正确的是( )
| A. | 方程3x-2=2x+1,移项得,3x-2x=-1+2 | |
| B. | 方程3-x=2-5( x-1),去括号得,3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}t=\frac{3}{2}$,系数化为1得,t=1 | |
| D. | 方程$\frac{x-1}{0.2}-\frac{x}{0.5}=1$,去分母得,5( x-1)-2x=1 |
15.下列数中,不是分数的是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 3.14 | C. | $\sqrt{\frac{4}{9}}$ | D. | $\root{3}{{\frac{1}{27}}}$ |
 作图题(要求尺规作图,不写作法,保留作图痕迹)
作图题(要求尺规作图,不写作法,保留作图痕迹)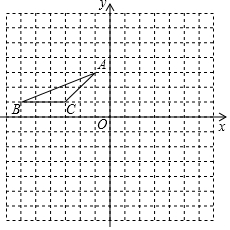 如图,平面直角坐标系中,每个小正方形边长都是1.
如图,平面直角坐标系中,每个小正方形边长都是1.