题目内容
如图，在?ABCD中，E，F是AD的三等分点，G，H是BC的三等分点，则图中共有平行四边形（ ）| A、3个 | B、4个 | C、5个 | D、6个 |
考点：平行四边形的判定
专题：
分析：本题主要依据平行四边形的性质及平行四边形的判定，解决问题．
解答：解：∵E、G是AD的三等分点，F、H是BC的三等分点，
∴AE=EG=GD=
AD，BF=FH=HC=
BC．
∵有平行四边形ABCD，
∴AD∥BC，AD=BC，
∴AE=EG=GD=BF=FH=HC，
∴图中的平行四边形共有6个，它们分别为：平行四边形ABCD，平行四边形ABFE，平行四边形ABHG，平行四边形EFHG，平行四边形EFCD，平行四边形GHCD．
故选D．
∴AE=EG=GD=
| 1 |
| 3 |
| 1 |
| 3 |
∵有平行四边形ABCD，
∴AD∥BC，AD=BC，
∴AE=EG=GD=BF=FH=HC，
∴图中的平行四边形共有6个，它们分别为：平行四边形ABCD，平行四边形ABFE，平行四边形ABHG，平行四边形EFHG，平行四边形EFCD，平行四边形GHCD．
故选D．
点评：本题主要考查平行四边形的性质及判定定理，解题的关键是熟练掌握平行四边形的判定定理．
练习册系列答案
金钥匙试卷系列答案
相关题目
如图，在平行四边形ABCD中，AD=4，AB=3，AE平分∠BAD交BC于点E，则线段BE，EC的长分别为（ ）| A、2与2 | B、3与1 |
| C、3与2 | D、1与3 |
函数y=-
与坐标轴的交点有（ ）
| 2 |
| x |
| A、0个 | B、1个 | C、2个 | D、4个 |
有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学知道自己的成绩后，要判断能否进入决赛，还需知道这9名同学成绩的（ ）
| A、众数 | B、中位数 |
| C、平均数 | D、方差 |
如图，有五个半圆，邻近的两个半圆均相切，两只小虫同时从点A出发，以相同的速度前往点B，甲虫沿着 | ||
AD
|
| ||||
|
| ||||
|
| ||
|
|
| ACB |
| A、甲先到达点B |
| B、乙先到达点B |
| C、甲、乙同时到达点B |
| D、无法确定 |
在平面直角坐标系中，将一个半径为2的圆的圆心P（0，y）沿y轴移动．已知⊙P与x轴相离，则y的取值范围是（ ）
| A、y＞2 |
| B、-2＜y＜2 |
| C、y＞2或y＜-2 |
| D、y＜-2 |
如图，在?ABCD中，若∠B=60°，AB=5cm，则以下结论正确的是（ ）| A、BC=5cm，∠D=60° | ||||
B、AD与BC之间的距离为
| ||||
C、AB与CD之间的距离为
| ||||
| D、∠A=120°，AD=5cm |
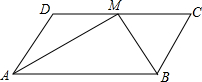如图，在平行四边形ABCD中，M是CD的中点，AB=2BC，BM=6，AM=8，则CD的长为（ ）| A、12 | B、10 | C、8 | D、6 |