题目内容
 如图,在?ABCD中,若∠B=60°,AB=5cm,则以下结论正确的是( )
如图,在?ABCD中,若∠B=60°,AB=5cm,则以下结论正确的是( )| A、BC=5cm,∠D=60° | ||||
B、AD与BC之间的距离为
| ||||
C、AB与CD之间的距离为
| ||||
| D、∠A=120°,AD=5cm |
考点:平行四边形的性质
专题:
分析:利用∠B的正弦求出AD、BC之间的距离,再根据平行四边形的对边相等,对角相等,邻角互补解答.
解答:解:∵∠B=60°,AB=5cm,
∴AD与BC之间的距离为:AB•sin60°=5×
=
cm,
BC、AD是AB的邻边,长度无法求解,CD=AB=5cm,
∠D=∠B=60°,∠A=∠C=180°-60°=120°,
纵观各选项,只有AD与BC之间的距离为
cm,CD=5cm正确.
故选B.
∴AD与BC之间的距离为:AB•sin60°=5×
| ||
| 2 |
5
| ||
| 2 |
BC、AD是AB的邻边,长度无法求解,CD=AB=5cm,
∠D=∠B=60°,∠A=∠C=180°-60°=120°,
纵观各选项,只有AD与BC之间的距离为
| 5 |
| 2 |
| 3 |
故选B.
点评:本题考查了平行四边形的性质,熟记平行四边形有关边和角的性质是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,E,F是AD的三等分点,G,H是BC的三等分点,则图中共有平行四边形( )
如图,在?ABCD中,E,F是AD的三等分点,G,H是BC的三等分点,则图中共有平行四边形( )| A、3个 | B、4个 | C、5个 | D、6个 |
某地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:34,35,36,34,36,37,36,37,37,37(单位:℃),则这组数据的中位数和众数分别是( )
| A、36℃,37℃ |
| B、37℃,36℃ |
| C、36.5℃,37℃ |
| D、37℃,36.5℃ |
由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)…求证:这个二次函数的图象关于直线x=2对称.根据现有信息,题中的二次函数不一定具有的性质是( )
| A、过点(3,0) |
| B、顶点是(-2,-2) |
| C、在x轴上截得的线段的长度是2 |
| D、c=3a |
要使分式
有意义,则x的取值范围是( )
| 3x |
| 3x-8 |
A、x=
| ||
B、x>
| ||
C、x<
| ||
D、x≠
|
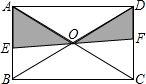 如图,矩形ABCD的对角线的交点为O,EF过点O且分别交AB,CD于点E,F,则图中阴影部分的面积是矩形ABCD的面积的( )
如图,矩形ABCD的对角线的交点为O,EF过点O且分别交AB,CD于点E,F,则图中阴影部分的面积是矩形ABCD的面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列光源形成的投影不同于其他三种的是( )
| A、太阳光 | B、灯光 |
| C、探照灯光 | D、台灯 |
 如图,矩形ABCD中,AE=BF=3,EF⊥ED交BC于点F,矩形的周长为22,求EF的长.
如图,矩形ABCD中,AE=BF=3,EF⊥ED交BC于点F,矩形的周长为22,求EF的长.