题目内容
在平面直角坐标系中,将一个半径为2的圆的圆心P(0,y)沿y轴移动.已知⊙P与x轴相离,则y的取值范围是( )
| A、y>2 |
| B、-2<y<2 |
| C、y>2或y<-2 |
| D、y<-2 |
考点:直线与圆的位置关系,坐标与图形性质
专题:
分析:本题应将该点的纵坐标与半径对比,大于半径时,则坐标轴与该圆相离,根据以上得出即可.
解答:解:分为两种情况:①当P在x轴的上方时,如果⊙P与x轴相离,那么y>2;
②当P在x轴的下方时,如果⊙P与x轴相离,那么y<-2;
故选C.
②当P在x轴的下方时,如果⊙P与x轴相离,那么y<-2;
故选C.
点评:本题考查了直线与圆的位置关系、坐标与图形性质,注意直线与圆相离,直线到圆的距离大于半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果一个平行四边形的周长为80cm,相邻两边的长度比为3:2,那么这个平行四边形的较短边长为( )
| A、16cm | B、24cm |
| C、32cm | D、48cm |
 如图,在?ABCD中,E,F是AD的三等分点,G,H是BC的三等分点,则图中共有平行四边形( )
如图,在?ABCD中,E,F是AD的三等分点,G,H是BC的三等分点,则图中共有平行四边形( )| A、3个 | B、4个 | C、5个 | D、6个 |
下列方程中,解为x=1±
的是( )
| 2 |
| A、x2-1=3 |
| B、(x+1)2=2 |
| C、(x-1)2=2 |
| D、(x-2)2=1 |
某地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:34,35,36,34,36,37,36,37,37,37(单位:℃),则这组数据的中位数和众数分别是( )
| A、36℃,37℃ |
| B、37℃,36℃ |
| C、36.5℃,37℃ |
| D、37℃,36.5℃ |
由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)…求证:这个二次函数的图象关于直线x=2对称.根据现有信息,题中的二次函数不一定具有的性质是( )
| A、过点(3,0) |
| B、顶点是(-2,-2) |
| C、在x轴上截得的线段的长度是2 |
| D、c=3a |
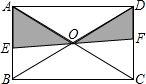 如图,矩形ABCD的对角线的交点为O,EF过点O且分别交AB,CD于点E,F,则图中阴影部分的面积是矩形ABCD的面积的( )
如图,矩形ABCD的对角线的交点为O,EF过点O且分别交AB,CD于点E,F,则图中阴影部分的面积是矩形ABCD的面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
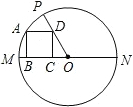 如图,已知在⊙O中,直径MN=10,四边形ABCD是正方形,并且∠POM=45°,则AB的长为
如图,已知在⊙O中,直径MN=10,四边形ABCD是正方形,并且∠POM=45°,则AB的长为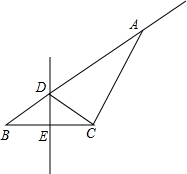 如图,在△ABC中,DE是边BC的垂直平分线,与边AB、BC交于点D、E,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪些线段的长?
如图,在△ABC中,DE是边BC的垂直平分线,与边AB、BC交于点D、E,如果△ACD的周长为17cm,△ABC的周长为25cm,根据这些条件,你可以求出哪些线段的长?