题目内容
20．因式分解：x2+6xy+9y2+2x+6y-3．分析 根据完全平方公式得出（x+3y）2+2（x+3y）-3，再用十字相乘法进行分解即可，注把x+3y看作整体．
解答 解：x2+6xy+9y2+2x+6y-3=（x+3y）2+2（x+3y）-3
=（x+3y-1）（x+3y-3）．
点评 本题考查了因式分解，掌握完全平方公式和十字相乘法是解题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知AB是⊙O的直径，BP是⊙O的弦，弦CD⊥AB于点F，交BP于点G，E在CD的延长线上，EP=EG．
15．某股民在上周星期五买进某种股票500股，每股60元，下表是本周股票的涨跌情况（单位：元）：
（1）本周星期五收盘时，每股是多少元？
（2）已知买进股票时付了0.15%的手续费，卖出股票时需付成交额0.15%的手续费和0.1%的交易费，若在本周五收盘前将全部股票一次性地卖出，他的收益如何？
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
（2）已知买进股票时付了0.15%的手续费，卖出股票时需付成交额0.15%的手续费和0.1%的交易费，若在本周五收盘前将全部股票一次性地卖出，他的收益如何？
5．不等式组$\left\{\begin{array}{l}{-3（x+1）-x＜5}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$的解为（ ）
| A． | x＜-2或x≥1 | B． | x＜-2 | C． | -2＜x≤1 | D． | -2$＜x＜\frac{1}{2}$ |
12．
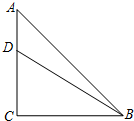如图，在等腰Rt△ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=$\frac{1}{5}$，则AD的长为（ ）
如图，在等腰Rt△ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=$\frac{1}{5}$，则AD的长为（ ）| A． | 1 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 2 |