题目内容
14. 如图,有一直径是$\sqrt{2}$的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为$\frac{1}{4}$米.
如图,有一直径是$\sqrt{2}$的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为$\frac{1}{4}$米.
分析 首先根据铁皮的半径求得AB的长,再设圆锥的底面圆的半径为r,则根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=$\frac{90π×1}{180}$,然后解方程即可.
解答 解:∵⊙O的直径BC=$\sqrt{2}$,
∴AB=$\frac{\sqrt{2}}{2}$BC=1,
设圆锥的底面圆的半径为r,
则2πr=$\frac{90π×1}{180}$,解得r=$\frac{1}{4}$,
即圆锥的底面圆的半径为$\frac{1}{4}$米.
故答案为:$\frac{1}{4}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
5.若三角形的两条边长分别为6cm和10cm,则它的第三边长不可能为( )
| A. | 5cm | B. | 8cm | C. | 10cm | D. | 17cm |
3. 如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
 如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )| A. | (40-x)(26-2x)=144×6 | B. | (40-2x)(26-x)=144×6 | C. | (40-2x)(26-x)=144÷6 | D. | (40-x)(26-2x)=144÷6 |
 如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为$\frac{18}{5}$.
如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为$\frac{18}{5}$.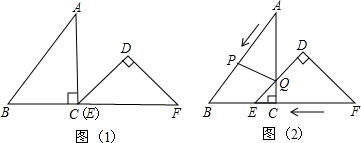
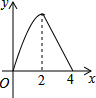
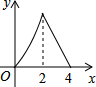
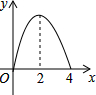
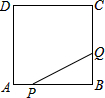 如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B-C-D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )
如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B-C-D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )

 如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.
如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.