题目内容
如图，⊙O的半径为2，以圆内接正方形ABCD的顶点B为圆心，AB为半径．画弧AC，则阴影部分的面积是考点：扇形面积的计算
专题：
分析：圆的面积减去正方形的面积，可将劣弧与正方形的每条边所围成的面积求出，阴影部分的面积为扇形ABC的面积加上劣弧与正方形的边所围成的面积的一半．
解答：解：∵⊙O的半径为2，
∴正方形的边长为2
；
劣弧与正方形的边所围成的面积为：π•22-（2
）2=4（π-2）
扇形的面积为：
=2π；
故阴影部分的面积为：2π+
×4（π-2）=4π-4．
故答案是：4π-4．
解：∵⊙O的半径为2，∴正方形的边长为2
| 2 |
劣弧与正方形的边所围成的面积为：π•22-（2
| 2 |
扇形的面积为：
90π(2
| ||
| 360 |
故阴影部分的面积为：2π+
| 1 |
| 2 |
故答案是：4π-4．
点评：本题考查了扇形面积的计算．求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．
练习册系列答案
阅读快车系列答案
相关题目
已知圆柱的母线长5，侧面积为30π，则圆柱的底面直径长是（ ）
| A、3 | B、6 | C、9 | D、12 |
如图，⊙O直径AB=8，∠CBD=30°，则CD=（ ）| A、4 | ||
| B、6 | ||
| C、3 | ||
D、2
|
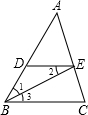请把下列说理过程补充完整：?已知：如图，DE∥BC，BE平分∠ABC．你能说明∠1=∠3吗？
理由：∵BE平分∠ABC（已知），
∴∠1=
又∵DE∥BC（已知），
∴∠2=
∴∠1=∠3（等量代换）．
二次函数y=x2-4x+3的图象与x轴的交点坐标是（ ）
| A、（1，0），（-3，0） |
| B、（1，0），（3，0） |
| C、（-1，0），（-3，0） |
| D、（3，0），（-1，0） |
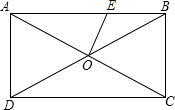如图，矩形ABCD中，AC交BD于O，∠AOD=60°，OE⊥AC，AD=