题目内容
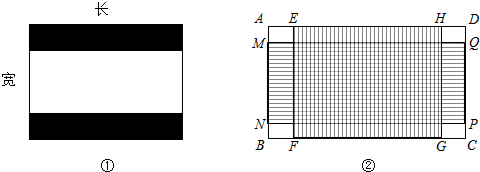
如图①,老旧电视机屏幕的长宽比为4:3,但是多数电影图象的长宽比为2.4:1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度):
①该屏幕的长= 寸,宽= 寸;
②已知“屏幕浪费比=
”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(矩形ABCD)恰好包含面积相等且长宽比分别为4:3的屏幕(矩形EFGH)与2.4:1的屏幕(矩形MNPQ).求这种屏幕的长宽比.(参考数据:
≈2.2,结果精确到0.1)
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度):
①该屏幕的长=
②已知“屏幕浪费比=
| 黑色带子的总面积 |
| 电视机屏幕的总面积 |
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(矩形ABCD)恰好包含面积相等且长宽比分别为4:3的屏幕(矩形EFGH)与2.4:1的屏幕(矩形MNPQ).求这种屏幕的长宽比.(参考数据:
| 5 |

考点:勾股定理的应用
专题:
分析:(1)①根据电视机屏幕的长宽比为4:3,设长为4x,则宽为3x,再由勾股定理求出x的值,进而可得出结论;
②设在该屏幕上播放长宽比为2.4:1的视频时,视频的宽为a寸(长为16寸),求出a的值,得出黑色带子的宽度,进而得出其比值;
(2)根据题意得出
=
,
=
,得PQ=
BC,FG=
EF.再由S矩形EFGH=S矩形MNPQ即可得出
=
,进而可得出结论.
②设在该屏幕上播放长宽比为2.4:1的视频时,视频的宽为a寸(长为16寸),求出a的值,得出黑色带子的宽度,进而得出其比值;
(2)根据题意得出
| PQ |
| BC |
| 1 |
| 2.4 |
| EF |
| FG |
| 3 |
| 4 |
| 5 |
| 12 |
| 4 |
| 3 |
| BC2 |
| EF2 |
| 16 |
| 5 |
解答:解:(1)①∵电视机屏幕的长宽比为4:3,
∴设长为4x,则宽为3x,
∵电视机屏幕为20寸,
∴(4x)2+(3x)2=202,解得x=4,
∴4x=16,3x=12,
∴该屏幕的长为16寸,宽为12寸;
故答案为:16;12.
②设在该屏幕上播放长宽比为2.4:1的视频时,视频的宽为a寸(长为16寸).
∵
=
,解得 a=
.
∴黑色带子的宽的和=12-
=
.
∴屏幕浪费比=
=
;
(2)由题意:
=
,
=
,得:PQ=
BC,FG=
EF.
∵S矩形EFGH=S矩形MNPQ,
∴BC•
BC=EF•
EF.
∴
=
,
∴
=
≈1.8.
答:这种屏幕的长宽比约为1.8.
∴设长为4x,则宽为3x,
∵电视机屏幕为20寸,
∴(4x)2+(3x)2=202,解得x=4,
∴4x=16,3x=12,
∴该屏幕的长为16寸,宽为12寸;
故答案为:16;12.
②设在该屏幕上播放长宽比为2.4:1的视频时,视频的宽为a寸(长为16寸).
∵
| 16 |
| 2.4 |
| a |
| 1 |
| 20 |
| 3 |
∴黑色带子的宽的和=12-
| 20 |
| 3 |
| 16 |
| 3 |
∴屏幕浪费比=
| ||
| 16×12 |
| 4 |
| 9 |
(2)由题意:
| PQ |
| BC |
| 1 |
| 2.4 |
| EF |
| FG |
| 3 |
| 4 |
| 5 |
| 12 |
| 4 |
| 3 |
∵S矩形EFGH=S矩形MNPQ,
∴BC•
| 5 |
| 12 |
| 4 |
| 3 |
∴
| BC2 |
| EF2 |
| 16 |
| 5 |
∴
| BC |
| EF |
| 4 | ||
|
答:这种屏幕的长宽比约为1.8.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
 张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,
张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x, 如图,⊙O的半径为2,以圆内接正方形ABCD的顶点B为圆心,AB为半径.画弧AC,则阴影部分的面积是
如图,⊙O的半径为2,以圆内接正方形ABCD的顶点B为圆心,AB为半径.画弧AC,则阴影部分的面积是