题目内容
2．观察下列各式：13=12，13+23=32，13+23+33=62，13+23+33=62，13+23+33+43=102，…，计算13+23+33+…+103的结果是（ ）| A． | 2025 | B． | 2500 | C． | 3025 | D． | 3600 |
分析 根据13=12，13+23=32，13+23+33=62，13+23+33+43=102，…，可得从1开始的连续自然数的立方和等于它们的和的平方，据此求出计算13+23+33+…+103的结果是多少即可．
解答 解：∵13=12，13+23=32=（1+2）2，13+23+33=62=（1+2+3）2，13+23+33+43=102=（1+2+3+4）2，
∴13+23+33+…+103=（1+2+3+…+10）2=552=3025．
故选：C．
点评 此题主要考查了有理数的混合运算，要熟练掌握，解答此题的关键是注意总结出规律，并能应用总结出的规律解决实际问题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10．已知（-3，y1），（0，y2），（3，y3）是抛物线y=-3x2+6x-k上的点，则（ ）
| A． | y1＜y2＜y3 | B． | y1＜y3＜y2 | C． | y3＜y1＜y2 | D． | y2＜y1＜y3 |
如图，在正方形网格中有一个三角形△ABC，在网格中画出△ABC绕点C逆时针旋转90°后得到△A1B1C1．
14．一元一次方程-3x+9=0的解就是一次函数y=-3x+9的图象与（ ）
| A． | x轴交点的横坐标 | B． | y轴交点的横坐标 | C． | x轴交点的纵坐标 | D． | y轴交点的纵坐标 |
11．
如图，菱形OBCD在平面直角坐标系中的位置如图所示，顶点B（0，2$\sqrt{3}$），∠DOB=60°，点P是对角线OC上的一个动点，已知A（-1，0），则AP+BP的最小值为（ ）
如图，菱形OBCD在平面直角坐标系中的位置如图所示，顶点B（0，2$\sqrt{3}$），∠DOB=60°，点P是对角线OC上的一个动点，已知A（-1，0），则AP+BP的最小值为（ ）| A． | 4 | B． | 5 | C． | 3$\sqrt{3}$ | D． | $\sqrt{19}$ |
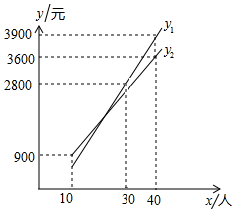2016年3月28日，农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路，其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选．已知河北省某旅游景点的门票为a元/人，为吸引团队游客，对团队10人以上（包含10人）的游客实行动态票价：节假日期间门票不打折，但会在团队总费用的基础上有优惠；非节假日期间门票打b折．某团队在节假日期间的门票总费用y1（元）、非节假日期间的门票总费用y2（元）与团队人数x（人）（x≥10）之间的函数关系的图象如图所示．