题目内容
1.在平行四边形ABCD中,对角线AC、BD相交于点O,且AC+BD=30,△OCD的周长为22,则AB的长度为7.分析 因为四边形ABCD是平行四边形,所以OA=OC,OB=OD,由AC+BD=30,推出2OD+2OC=30,推出OD+OC=15,由△OCD的周长为22,即可求出CD解决问题.
解答 解:如图,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AC+BD=30,
∴2OD+2OC=30,
∴OD+OC=15,
∵△OCD的周长为22,
∴AB=CD=22-15=7,
故答案为7.
点评 本题考查平行四边形的性质、三角形的周长等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
11.在$\frac{1}{3}$ab-$\frac{1}{4}$ac、$\frac{x}{x+y}$、$\frac{1}{π}$、1-$\frac{1}{x}$中,分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.如图,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是正方形.
如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是正方形.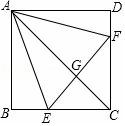 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC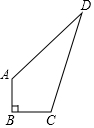 在四边形ABCD中,AB=3,BC=4,CD=13,DA=12,且∠B=90°.求四边形ABCD 的面积.
在四边形ABCD中,AB=3,BC=4,CD=13,DA=12,且∠B=90°.求四边形ABCD 的面积.