题目内容
18.对有理数a、b规定一种新运算“△”:a△b=|a-2b|.例:(-2)△3=|(-2)-2×3|=8,则:
(1)0△(-4)=8;
(2)(1△2)△3<1△(2△3).(用“=”或“≠”填空)
分析 (1)根据△的含义,以及有理数的混合运算的运算方法,求出0△(-4)的值是多少即可.
(2)根据△的含义,可得(1△2)△3,1△(2△3)的值,再比较大小即可求解.
解答 解:(1)0△(-4)
=|0-2×(-4)|
=|0+8|
=8;
(2)∵(1△2)△3
=|1-2×2|△3
=|1-4|△3
=3△3
=|3-2×3|=|3-6|
=6,
1△(2△3)
=1△|2-2×3|
=1△|2-6|
=1△4
=|1-2×4|
=|1-8|
=7,
6<7,
∴(1△2)△3<1△(2△3).
故答案为:8;<.
点评 此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

练习册系列答案
相关题目
8.在-2,$\sqrt{4}$,$\sqrt{2}$,3.14这4个数中,无理数是( )
| A. | -2 | B. | $\sqrt{4}$ | C. | $\sqrt{2}$ | D. | 3.14 |
6.如图,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
13.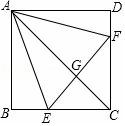 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
.其中正确结论有( )
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC.其中正确结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列计算正确的是( )
| A. | a3+a4=a7 | B. | a3•a4=a12 | C. | (a3)4=a12 | D. | a4-a3=a |
7.x=2时,px3+qx+1=2012,则x=-2时,代数式px3+qx+1的值为( )
| A. | 2011 | B. | -2012 | C. | -2010 | D. | 2013 |
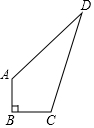 在四边形ABCD中,AB=3,BC=4,CD=13,DA=12,且∠B=90°.求四边形ABCD 的面积.
在四边形ABCD中,AB=3,BC=4,CD=13,DA=12,且∠B=90°.求四边形ABCD 的面积.