题目内容
15. 如图,在△ABC中,已知∠B=∠C=30°,EF垂直平分AC于点E,交BC于点F.若FC=3,则BF=6.
如图,在△ABC中,已知∠B=∠C=30°,EF垂直平分AC于点E,交BC于点F.若FC=3,则BF=6.
分析 连接AF,先由三角形内角和定理得出∠BAC的度数,再由线段垂直平分线的性质得出CF=AF,∠CAF=∠C=30°,故可得出∠BAF的度数,根据直角三角形的性质即可得出结论.
解答  解:连接AF,
解:连接AF,
∵∠B=∠C=30°,
∴∠BAC=180°-30°-30°=120°.
∵EF垂直平分AC于点E,交BC于点F,FC=3,
∴CF=AF=3,∠CAF=∠C=30°,
∴∠BAF=∠BAC-∠CAF=120°-30°=90°,
∴BF=2AF=6.
故答案为:6.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
5.若关于x的不等式2+2x<m的正整数解为1和2,则m的取值范围是( )
| A. | 6<m≤8 | B. | 6≤m≤8 | C. | 6<m<8 | D. | 6≤m<8 |
10.已知等腰三角形的一边为2,一边为5,那么它的周长等于( )
| A. | 9 | B. | 12 | C. | 9或12 | D. | 7或10 |
20.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工王师傅2013年月退休金为1800元,2015年达到2460元.设王师傅的月退休金从2013年到2015年年平均增长率为x,可列方程为( )
| A. | 2460(1-x)2=1800 | B. | 1800(1+x)2=2460 | ||
| C. | 1800(1-x)2=2460 | D. | 1800+1800(1+x)+1800(1+x)2=2460 |
4.若分式$\frac{{x}^{2}-x-6}{{x}^{2}+3x+2}$的值为0,则x的值为( )
| A. | 3或-2 | B. | 3 | C. | -2 | D. | -3或2 |
 如图,从点O引出6条射线OA,OB,OC,OD,OE,OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD度数.
如图,从点O引出6条射线OA,OB,OC,OD,OE,OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD度数.

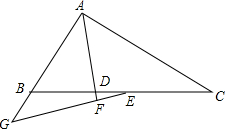 已知,△ABC中,AD是角平分线,点E在BC上,EF⊥AD交AD、AB于F、G.
已知,△ABC中,AD是角平分线,点E在BC上,EF⊥AD交AD、AB于F、G.