题目内容
15.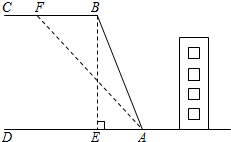 如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:$\frac{5}{12}$,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.
如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:$\frac{5}{12}$,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长.
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75).
分析 (1)根据坡度的概念得到BE:EA=12:5,根据勾股定理计算列式即可;
(2)作FH⊥AD于H,根据正切的概念求出AH,结合图形计算即可.
解答 解:(1)∵斜坡AB的坡比为i=1:$\frac{5}{12}$,
∴BE:EA=12:5,
设BE=12x,则EA=5x,
由勾股定理得,BE2+EA2=AB2,即(12x)2+(5x)2=262,
解得,x=2,
则BE=12x=24,AE=5x=10,
答:改造前坡顶与地面的距离BE的长为24米;
(2)作FH⊥AD于H,
则tan∠FAH=$\frac{FH}{AH}$,
∴AH=$\frac{24}{1.33}$≈18,
∴BF=18-10=8,
答:BF至少是8米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.平面直角坐标系中,正六边形ABCDEF的起始位置如图1所示,边AB在x轴上,现将正六边形沿x轴正方向无滑动滚动,第一次滚动后,边BC落在x轴上(如图2);第二次滚动后,边CD落在x轴上,如此继续下去.则第2016次滚动后,落在x轴上的是( )


| A. | 边DE | B. | 边EF | C. | 边FA | D. | 边AB |
3.如果单项式2anb2c是六次单项式,那么n的值取( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
3.用半径为12cm,圆心角为150°的扇形做一个圆锥模型的侧面,则此圆锥底面圆的半径为( )
| A. | 5cm | B. | 30cm | C. | 6cm | D. | 10cm |
1.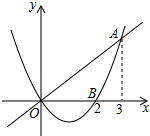 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
 如图,O点在直线AB上,∠AOD=90°,∠COE=90°,则图中相等的锐角有2对.
如图,O点在直线AB上,∠AOD=90°,∠COE=90°,则图中相等的锐角有2对.