Question

5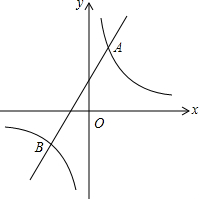．已知一次函数y₁=ax+b与反比例函数y₂=$\frac{k}{x}$交于点A（1，4）和点B（m，-2）．
（1）求这两个函数的表达式；
（2）根据图象直接写出当y₁＜y₂时，自变量x的取值范围；
（3）如果点C与点A关于x轴对称，求△ABC的面积．

Answer 1

分析 （1）把点A坐标代入反比例函数求出m的值，也就求出了反比例函数解析式，再把点B的坐标代入反比例函数解析式求出n的值，得到点B的坐标，然后利用待定系数法即可求出一次函数解析式；
（2）找出直线在反比例函数图形的下方的自变量x的取值即可；
（3）根据轴对称的性质求得C的坐标，过B点作BD⊥AC于D，求得AC、BD的长，根据三角形面积公式求得即可．

解答 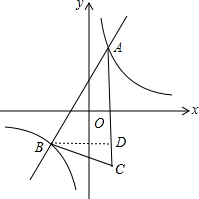解：（1）∵点A（1，4）在反比例函数y₂=$\frac{k}{x}$的图象上，
∴k=1×4=4，
∴反比例函数的表达式为y₂=$\frac{4}{x}$，
∵点B（m，-2）也在反比例函数y₂=$\frac{4}{x}$的图象上，
∴-2=$\frac{4}{m}$，解得m=-2
即B（-2，-2），
把点A（1，4），点B（-2，-2）代入一次函数y₁=kx+b中，
得$\left\{\begin{array}{l}{a+b=4}\\{-2a+b=-2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$，
∴一次函数的表达式为y₁=2x+2；
故一次函数得到解析式为y₁=2x+2，反比例函数解析式为y₂=$\frac{4}{x}$；

（2）当0＜x＜1或x＜-2时，y₁＜y₂；

（3）如图，过B点作BD⊥AC于D，
∵点C与点A关于x轴对称，
∴C（1，-4），
∴AC=8，BD=3，
∴S_△ABC=$\frac{1}{2}$AC•BD=12．

点评 本题考查了反比例函数与一次函数的交点问题，待定系数法求函数解析式，轴对称的性质以及三角形面积，此类题目的求解一般都是先把已知点的坐标代入反比例函数表达式求出反比例函数解析式，然后再求一次函数解析式，难度中等．