题目内容
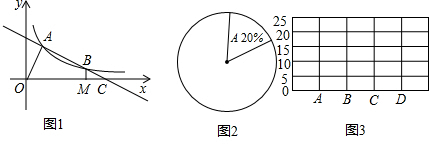
16.如图1,直线AB交双曲线y=$\frac{k}{x}$于点A,B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连接OA,若OM=2MC,S△OAC=12,则k的值为( )A.6 B.8 C.12 D.24
九年级一班的数学老师在考后分析试卷时对本班解答此题的情况进行了统计.四种答案的人数分别为:选A的10人占班内总人数的百分比如图2所示,选答案B的人数比答案C的少5人,选答案D的人数是选答案C的人数的四分之一.
(1)求选择答案B,C,D的人数;
(2)请你补全扇形统计图2,然后在图3中画出折线图;
(3)对于这道期末考试题,请你给出正确的选项,并写出解析.
分析 (1)根据选A的人数及在扇形中所占的比例即可得出九年级一班的学生总数,设选答案C的人数为x,则选答案B的人数为(x-5)人,选答案D的人数为$\frac{1}{4}$x人,根据题意列出方程即可求得.
(2)用选各答案的人数除以总人数得出百分比,再画图即可解答.
(3)连结OB,设B点坐标为(a,b),将B点坐标代入反比例解析式得到ab=k,确定出OM与BM的长,根据OM=2MC,表示出MC长,进而表示出三角形BOM与三角形BMC的面积,两面积之和表示出三角形BOC的面积,由AB=BC,确定出三角形AOC的面积,由S△OAC=12列出关于k的方程,解方程即可求出k的值.
解答 解:(1)九年级一班学生总数=10÷20%=50人,
选答案B、C、D的总人数=50-10=40人,
设选答案C的人数为x,则选答案B的人数为(x-5)人,选答案D的人数为$\frac{1}{4}$x人,
根据题意得:x+x-5+$\frac{1}{4}$x=40,解得x=20,
x-5=15(人),$\frac{1}{4}$x=5(人)
答:选择答案B,C,D的人数分别为15、20、5人.
(2)如图所示: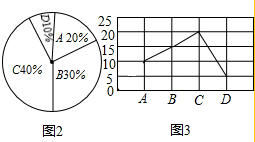
(3)B;
如图1,连结OB,
设B(a,b).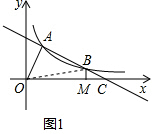 ∵点B在函数y=$\frac{k}{x}$上,
∵点B在函数y=$\frac{k}{x}$上,
∴ab=k,且OM=a,BM=b,
∵OM=2MC,
∴MC=$\frac{1}{2}$a,
∴S△BOM=$\frac{1}{2}$ab=$\frac{1}{2}$k,S△BMC=$\frac{1}{2}$×$\frac{1}{2}$ab=$\frac{1}{4}$ab=$\frac{1}{4}$k,
∴S△BOC=S△BOM+S△BMC=$\frac{1}{2}$k+$\frac{1}{4}$k=$\frac{3}{4}$k,
∵AB=BC,
∴S△AOB=S△BOC=$\frac{3}{4}$k,
∴S△AOC=S△AOB+S△BOC=$\frac{3}{2}$k,
∵S△AOC=12,
∴$\frac{3}{2}$k=12,
∴k=8.
故选B.
点评 此题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数的性质是解本题的关键.也考查的是折线图和扇形统计图的综合运用.

| A. | 7cm | B. | 12cm | C. | 1cm | D. | 7cm或1cm |
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
 小亮家最近买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知,用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)y分别作了预算,通过列表,并用x(㎡)表示铺设地面的面积,用y(元)表示铺设费用制成图.请你根据图4中所提供的信息,解答下列问题:
小亮家最近买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知,用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)y分别作了预算,通过列表,并用x(㎡)表示铺设地面的面积,用y(元)表示铺设费用制成图.请你根据图4中所提供的信息,解答下列问题: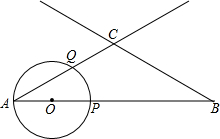 如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.
如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.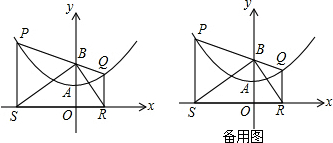
 矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?
矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?