Question

问题：在中，，∠A=100°，BD为∠B 的平分线，探究AD、BD、BC之间的数量关系.

请你完成下列探究过程：

（1）观察图形，猜想AD、BD、BC之间的数量关系为                         .

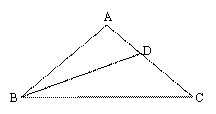（2）在对（1）中的猜想进行证明时，当推出∠ABC=∠C=40°后，可进一步推出∠ABD=∠DBC=           度.

（3）为了使同学们顺利地解答本题（1）中的猜想，小强同学提供了一种探究的思路：在BC上截取BE=BD，连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路，画出图形，在此基础上对（1）中的猜想加以证明.也可以选用其它的方法证明你的猜想.

Answer 1

解：（1）AD+BD=BC

（2）20

(3)画出图形

继续证明：在BC上截取BF=BA，连接DF,

∵∠ABD=∠DBC，BD=BD，∴△ABD≌△FBD，

∴AD=DF，①

∵∠A=100°，∴∠DFB=∠A=100°，∴∠DFC=80°，

∵BE=BD，∠DBC=20°,

∴∠BED =∠BDE =80°，∠DFE =∠FED,

∴DF=DE，②

∵∠FED=80°，∠C=40°，∴∠EDC=40°，

∴∠EDC =∠C，∴DE =EC，③

∴AD =EC，∴AD+BD=BC.  

（其它方法对应给分）.