题目内容
4.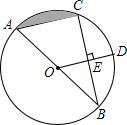 如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=2$\sqrt{3}$,DE=1,求:
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=2$\sqrt{3}$,DE=1,求:(1)⊙O的半径;
(2)弦AC的长;
(3)阴影部分的面积.
分析 (1)半径OD⊥BC,所以由垂径定理知:CE=BE,在直角△OCE中,根据勾股定理就可以求出OC的值;
(2)根据AB是⊙O的直径,得到∠ACB=90°,因而在直角三角形ABC中根据勾股定理得到AC的长;
(3)阴影部分的面积就是扇形OCA的面积减去△OAC的面积.
解答 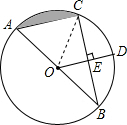 解:(1)连接OC,
解:(1)连接OC,
∵半径OD⊥BC,
∴CE=BE,
∵BC=2$\sqrt{3}$,
∴CE=$\sqrt{3}$,
设OC=x,在直角三角形OCE中,OC2=CE2+OE2,
∴x2=($\sqrt{3}$)2+(x-1)2,
∴x=2
即⊙O的半径为2;
(2)∵AB为直径,
∴∠ACB=90°,AB=4,
又∵BC=2$\sqrt{3}$,
∴AC2=AB2-BC2=4,
∴AC=2;
(3)∵OA=OC=AC=2,
∴∠AOC=60°,
∴S阴=S扇-S△OAC=$\frac{60π×{2}^{2}}{360}$-$\frac{1}{2}$×2×2×$\frac{\sqrt{3}}{2}$=$\frac{2}{3}$π-$\sqrt{3}$.
点评 本题考查了垂径定理,勾股定理以及扇形面积的计算.计算阴影部分的面积时,采用了“分割法”求得的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列运算正确的是( )
| A. | a-(b-c)=a-b-c | B. | a-(b-c)=a+b-c | C. | a-(b-c)=a+b+c | D. | a-(b-c)=a-b+c |
 在⊙O中,直径AB=4,弦CD⊥AB于P,OP=$\sqrt{3}$,则弦CD的长为2.
在⊙O中,直径AB=4,弦CD⊥AB于P,OP=$\sqrt{3}$,则弦CD的长为2.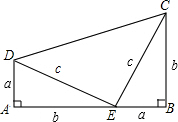 如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.