题目内容
2.(1)解不等式:2(x+1)-1≥3x+2,并把解集表示在数轴上.(2)解不等式组$\left\{\begin{array}{l}{3x+2≥2(x-1)}\\{1-\frac{x-1}{6}>\frac{x}{3}}\end{array}\right.$,并写出不等式组的整数解.
分析 (1)去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可;
(2)先求出每个不等式的解集,再求出不等式组的解集,最后求出整数解即可.
解答 解:(1)2(x+1)-1≥3x+2,
2x+2-1≥3x+2
2x-3x≥2-2+1
-x≥1,
x≤-1,
在数轴上表示不等式的解集为: ;
;
(2)$\left\{\begin{array}{l}{3x+2≥2(x-1)①}\\{1-\frac{x-1}{6}>\frac{x}{3}②}\end{array}\right.$
∵解不等式①得:x≥-4,
解不等式②得:x<$\frac{7}{3}$
∴不等式组的解集为:-4≤x<$\frac{7}{3}$,
∴不等式组的整数解为:-4,-3,-2,-1,0,1,2.
点评 本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解,在数轴上表示不等式的解集的应用,能正确解不等式和能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
10.关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:
①2a+b<0;
②ab<0;
③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;
④抛物线y=2x2+ax+b-2的顶点在第四象限.
其中正确的结论有( )
①2a+b<0;
②ab<0;
③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;
④抛物线y=2x2+ax+b-2的顶点在第四象限.
其中正确的结论有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
17.若x<y成立,则下列不等式成立的是( )
| A. | -x+2<-y+2 | B. | 4x>4y | C. | x-2<y-2 | D. | -3x<-3y |
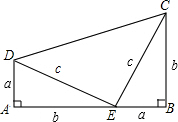 如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性. 若△ABC∽△ADE,AD=3,AB=5,DE=4,求BC的长.
若△ABC∽△ADE,AD=3,AB=5,DE=4,求BC的长. 有理数a,b,c在数轴上的位置如图所示,化简|c-b|+|a-c|+|b-c|.
有理数a,b,c在数轴上的位置如图所示,化简|c-b|+|a-c|+|b-c|.