题目内容
19.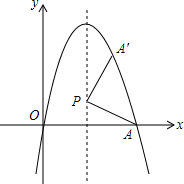 如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.
如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.(1)求点A的坐标及抛物线的顶点坐标;
(2)P是抛物线对称轴上的任意一点,将线段PA绕点P沿逆针方向旋转90°得到线段PA′,若点A′恰好落在抛物线上,求点P的坐标.
分析 (1)令y=0得-x2+6x=0,求得方程的解,从而得到点A的坐标,利用配方法求得抛物线的顶点坐标即可;
(2)过点A′作A′B⊥PC,垂足为B.先证明△PBA′≌△ACP于是得到PC=A′B,AC=PB=3,点P的坐标为(3,a),则点A′的坐标为(3+a,3+a).将点A′的坐标代入抛物线的解析式可求得a=2或a=-3,从而可求得点P的坐标为(3,2)或(3,-3).
解答 解:(1)令y=0得:-x2+6x=0,
解得:x1=0,x2=6.
y=-x2+6x=-(x2-6x+9-9)=-(x-3)2+9.
∴顶点坐标为(3,9).
(2)如图所示,过点A′作A′B⊥PC,垂足为B.
∵∠APA′是直角三角形,
∴∠APA′=90°.
∴∠A′PB+∠APC=90°.
又∵∠PAC+∠APC=90°,
∴∠A′PB=∠PAC.
在△PBA′和△ACP中,$\left\{\begin{array}{l}{∠A′BP=∠PCA=90°}\\{∠A′PB=∠PAC}\\{PA′=PA}\end{array}\right.$,
∴△PBA′≌△ACP.
∴PC=A′B,AC=PB=3.
设点P的坐标为(3,a),则点A′的坐标为(3+a,3+a).
将点A′的坐标代入抛物线的解析式得:-(3+a)2+6(3+a)=3+a.
解得:a=2或a=-3.
∴点P的坐标为(3,2)或(3,-3).
点评 本题主要考查的是求二次函数的解析式,全等三角形的性质和判定,利用全等三角形的性质得到点A的坐标(含字母a的式子)是解题的关键.

练习册系列答案
相关题目
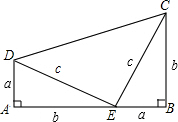 如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.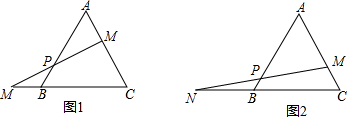
 若△ABC∽△ADE,AD=3,AB=5,DE=4,求BC的长.
若△ABC∽△ADE,AD=3,AB=5,DE=4,求BC的长.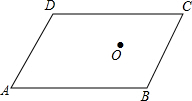 如图,O是?ABCD内一点,以O为位似中心,作?ABCD的位似图形,使?ABCD的边长缩小到原来的$\frac{1}{2}$.
如图,O是?ABCD内一点,以O为位似中心,作?ABCD的位似图形,使?ABCD的边长缩小到原来的$\frac{1}{2}$. 如图,在△ABC中,点D为边AB上一点,点F为BC延长线上一点,且AD=CF,连结DF,与AC相交于点E,点G为AC上一点,DG∥BC,△ADG∽△ABC,△EDG∽△EFC,那么$\frac{AB}{BC}$=$\frac{EF}{DE}$吗?为什么?
如图,在△ABC中,点D为边AB上一点,点F为BC延长线上一点,且AD=CF,连结DF,与AC相交于点E,点G为AC上一点,DG∥BC,△ADG∽△ABC,△EDG∽△EFC,那么$\frac{AB}{BC}$=$\frac{EF}{DE}$吗?为什么?