题目内容
在平面直角坐标系中,已知点M(-4,2),点N(2,-6),点P在y轴上,且PM=PN,求P点坐标.
考点:两点间的距离公式
专题:
分析:设出点P的坐标,运用两点间的距离公式列出方程,即可解决问题.
解答:解:设点P的坐标为P(0,λ),
∵PM=PN,
∴PM2=PN2,即:
(-4-0)2+(2-y)2=(2-0)2+(-6-y)2,
解得:y=-
,
即点P的坐标为P(0,-
).
∵PM=PN,
∴PM2=PN2,即:
(-4-0)2+(2-y)2=(2-0)2+(-6-y)2,
解得:y=-
| 5 |
| 4 |
即点P的坐标为P(0,-
| 5 |
| 4 |
点评:该题主要考查了两点间的距离公式及其应用问题;准确设出所求点的坐标是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
以下列各组数据为三角形的三边长,能构成直角三角形的是( )
| A、2cm,3cm,4cm |
| B、3cm,5cm,6cm |
| C、2cm,6cm,40cm |
| D、6cm,8cm,10cm |
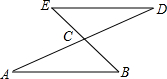 如图,AC=DC,BC=EC,求证:DE∥AB.
如图,AC=DC,BC=EC,求证:DE∥AB.