题目内容
11.如图1,以平行四边形ABCD的边AD、BC为边分别向外作等边三角形ADE和BCF.
(1)求证:四边形DEBF是平行四边形;
(2)如图2,如果再以AB、CD为边分别向外作等边三角形ABG和CDH,试判断四边形EGFH的形状,并说明理由.
(3)在(2)的条件下,若四边形EGFH为菱形,则四边形ABCD还需要满足什么条件?请说明理由.
分析 (1)根据平行四边形的判定方法:两组对边相等的四边形是平行四边形即可证明四边形DEBF是平行四边形.
(2)同理可证四边形AGCH是平行四边形,只要证明EF与GH互相平分即可.
(3)当四边形ABCD是矩形时,四边形EGFH是菱形,只要证明△EDH≌△FCH即可判断.
解答 (1)证明:如图1中,
∵四边形ABCD是平行四边形,
∴AD=BC,DC=AB,∠DAB=∠DCB,
∵以AD、BC为边分别向外作等边△ADE和等边△BCF,
∴AD=DE=AE,BF=BC,
∴AE=CF,
∵∠EAB=∠DAB+∠DAE,∠DCF=∠DCB+∠BCF,
∴∠EAB=∠DCF,
在△EAB和△DCF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠EAB=∠DCF}\\{AB=DC}\end{array}\right.$,
∴△EAB≌△DCF(SAS),
∴BE=FD,
∴四边形DEBF是平行四边形.
(2)如图2中,连接AH、CG、EF、AC、BD,
由(1)可知四边形DEBF是平行四边形,
∴EF与BD互相平分,
同理可证四边形AGCH是平行四边形,
∴AC与GH互相平分,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴EF与GH互相平分,
∴四边形EGFH是平行四边形.
(3)如图3中,当四边形ABCD是矩形时,四边形EGFH是菱形.
理由:∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,
∵∠EDA=∠HDC=∠HCD=∠BCF=60°,
∴∠EDH=∠HCF=150°,
在△EDH和△FCH中,
$\left\{\begin{array}{l}{DE=CF}\\{∠EDH=∠FCH}\\{DH=HC}\end{array}\right.$,
∴△EDH≌△FCH,
∴HE=HF,
∵四边形EGFH是平行四边形,
∴四边形EGFH是菱形.
点评 本题考查四边形综合题、全等三角形的判定和性质、平行四边形的判定和性质、菱形的判定、矩形的性质等知识,解题的关键是熟练应用这些知识解决问题,学会添加常用辅助线解决问题,属于中考常考题型.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案| A. | 若|a|=|b|,则a=b | B. | 若a<b,则|a|<|b| | ||
| C. | 若a、b互为相反数,则$\frac{a}{b}$=-1 | D. | 若a>|b|,则a>b |
 如图所示,△ABC≌△EFC,且BC⊥AC,若S△ABC=12cm2,CE=4cm,则BC的长为6cm.
如图所示,△ABC≌△EFC,且BC⊥AC,若S△ABC=12cm2,CE=4cm,则BC的长为6cm.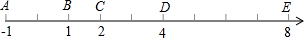 如图,在一条数轴上有依次排列的5台机床A、B、C、D、E在工作,现要设置一个零件供应站P,使这5台机床到供应站P的距离总和最小,供应站P建在哪?最小值为多少?
如图,在一条数轴上有依次排列的5台机床A、B、C、D、E在工作,现要设置一个零件供应站P,使这5台机床到供应站P的距离总和最小,供应站P建在哪?最小值为多少?