题目内容
6.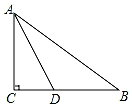 如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=5cm,AB=12cm,则△ABD的面积是30cm2.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=5cm,AB=12cm,则△ABD的面积是30cm2.
分析 作DE⊥AB,垂足为E,DE即为D到AB的距离.由角平分线的性质证得DE=DC.在△ABC中,由勾股定理求得AB=10,设CD=x,则DE=CD=x,BD=8-x.AE=AC=6,则BE=4,在Rt△BED中由勾股定理列出x2+42=(8-x)2,求得x的值,然后根据三角形的面积公式即可得到结论.
解答 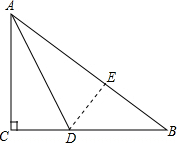 解:作DE⊥AB,垂足为E,DE即为D到AB的距离.
解:作DE⊥AB,垂足为E,DE即为D到AB的距离.
又∵∠C=90°,AD平分∠CAB,
∴DE=DC=5cm,
∴S△ABD=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×12×5=30cm2.
故答案为:30.
点评 本题考查了角平分线的性质,由已知能够注意到D到AB的距离即为DE长是解决的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.将抛物线y=-2(x+1)2-2向左平移2个单位,向下平移3个单位后的新抛物线解析式为( )
| A. | y=-2(x-1)2+1 | B. | y=-2(x+3)2-5 | C. | y=-2(x-1)2-5 | D. | y=-2(x+3)2+1 |
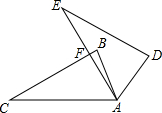 如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转50°得到△ADE,AE与BC交于F,则∠AFB=80°.
如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转50°得到△ADE,AE与BC交于F,则∠AFB=80°. 如图是一个几何体的表面展开图,图中的数字表示相应的棱的长度(单位:cm)
如图是一个几何体的表面展开图,图中的数字表示相应的棱的长度(单位:cm)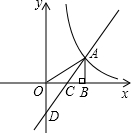 如图所示,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AOD=4.
如图所示,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AOD=4.