题目内容
1.化简(1)3a3b2÷a2+b(a2b-3ab);
(2)$\frac{x+2}{{x}^{2}-6x+9}$÷$\frac{1}{3-x}$•$\frac{x-3}{x+2}$.
分析 (1)原式利用单项式除以单项式,以及单项式乘以多项式法则计算,合并即可得到结果;
(2)原式利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=3ab2+a2b2-3ab2=a2b2;
(2)原式=-$\frac{x+2}{(x-3)^{2}}$•(x-3)•$\frac{x-3}{x+2}$=-1.
点评 此题考查了分式的乘除法,单项式乘多项式,以及整式的除法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知 $\sqrt{a-3}$•$\sqrt{a-5}$=$\sqrt{(a-3)(a-5)}$成立,则a 的取值范围是( )
| A. | a≥3 | B. | a≥5 | C. | a>3 | D. | a>5 |
11.已知在?ABCD中,∠A=80°,则∠B的度数是( )
| A. | 100° | B. | 160° | C. | 80° | D. | 60° |
 如图,四边形ABCD是矩形(AD>AB),请用直尺和圆规在边AD上找一点P,使得BP=2AB.(不写作法,保留作图痕迹)
如图,四边形ABCD是矩形(AD>AB),请用直尺和圆规在边AD上找一点P,使得BP=2AB.(不写作法,保留作图痕迹)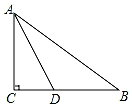 如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=5cm,AB=12cm,则△ABD的面积是30cm2.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=5cm,AB=12cm,则△ABD的面积是30cm2.