题目内容
 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,⊙O的切线AP与OC的延长线相交于点P,若PO=6cm,求AC的长.
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,⊙O的切线AP与OC的延长线相交于点P,若PO=6cm,求AC的长.考点:切线的性质
专题:计算题
分析:先根据圆周角定理得到∠AOC=2∠B=60°,则可判断△OAC为等边三角形,所以AC=OA,再根据切线的性质得到∠OAP=90°,然后在Rt△OAP中利用含30度的直角三角形三边的关系求出OA,从而得到AC的长.
解答:解:∵∠B=30°,
∴∠AOC=2∠B=60°,
而OC=OA,
∴△OAC为等边三角形,
∴AC=OA,
∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
在Rt△OAP中,∵∠AOP=60°,
∴∠P=30°,
∴OA=
OP=
×6=3,
∴AC=3cm.
∴∠AOC=2∠B=60°,
而OC=OA,
∴△OAC为等边三角形,
∴AC=OA,
∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
在Rt△OAP中,∵∠AOP=60°,
∴∠P=30°,
∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC=3cm.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
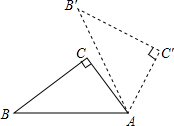 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )| A、π | ||
B、
| ||
C、
| ||
D、
|
 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则cosC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则cosC等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图是一个几何体的主视图和俯视图,求该几何体的体积.(π取3.14)
如图是一个几何体的主视图和俯视图,求该几何体的体积.(π取3.14) 已知AB=8,C、D为线段AB上任意两点,且CD=3,E为AC中点,F为BD中点,求EF的长度.
已知AB=8,C、D为线段AB上任意两点,且CD=3,E为AC中点,F为BD中点,求EF的长度. 已知,如图,在△ABC中,AB=8,BC=20,BC边上的中线AD=6,则△ADC的面积
已知,如图,在△ABC中,AB=8,BC=20,BC边上的中线AD=6,则△ADC的面积