题目内容
某超市销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱的售价在40元~70元之间.市场调查发现:若每箱50元销售,平均每天可销售90箱,价格每降低1元,平均每天多销售3箱;价格每升高1元,平均每天少销售3箱.
(1)写出平均每天的销售量y(箱)与每箱售价x(元)之间的函数关系式(注明自变量x的取值范围);(2)求出超市平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数关系式(每箱的利润=售价-进价);
(3)请把(2)中所求出的二次函数配方成w=a(x+
)2+
的形式,并指出当x=40、70时,W的值.
(4)在坐标系中画出(2)中二次函数的图象,请你观察图象说明:当牛奶售价为多少时,平均每天的利润最大?最大利润为多少?
(1)写出平均每天的销售量y(箱)与每箱售价x(元)之间的函数关系式(注明自变量x的取值范围);(2)求出超市平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数关系式(每箱的利润=售价-进价);
(3)请把(2)中所求出的二次函数配方成w=a(x+
| b |
| 2a |
| 4ac-b2 |
| 4a |
(4)在坐标系中画出(2)中二次函数的图象,请你观察图象说明:当牛奶售价为多少时,平均每天的利润最大?最大利润为多少?
考点:二次函数的应用
专题:
分析:(1)先分类:当40≤x≤50,y=90+3(50-x);当50<x≤70,y=90-3(x-50),综合得到y=-3x+240(40≤x≤70);
(2)平根据均每天销售这种牛奶的利润等于每箱的利润×销售量得到W=(x-40)•y,把y=-3x+240代入整理即可;
(3)把W=-3x2+360x-9600配成顶点式为W=-3(x-60)2+1200,则可确定顶点坐标;把x=40和70分别代入计算,求出对应的W的值;然后根据x的范围画草图;
(4)观察图象,找到顶点即可知道当牛奶售价为多少时,平均每天的利润最大,最大利润为多少.
(2)平根据均每天销售这种牛奶的利润等于每箱的利润×销售量得到W=(x-40)•y,把y=-3x+240代入整理即可;
(3)把W=-3x2+360x-9600配成顶点式为W=-3(x-60)2+1200,则可确定顶点坐标;把x=40和70分别代入计算,求出对应的W的值;然后根据x的范围画草图;
(4)观察图象,找到顶点即可知道当牛奶售价为多少时,平均每天的利润最大,最大利润为多少.
解答:解:(1)当40≤x≤50,y=90+3(50-x)=-3x+240;
当50<x≤70,y=90-3(x-50)=-3x+240,
∴平均每天销售量y(箱)与每箱售价x(元)之间的函数关系式为:y=-3x+240(40≤x≤70);
(2)W=(x-40)•y
=(x-40)(-3x+240)
=-3x2+360x-9600,
∴平均每天销售这种牛奶的利润W(元),与每箱牛奶的售价x(元)之间的二次函数关系式为W=-3x2+360x-9600(40≤x≤70);

(3)W=-3x2+360x-9600
=-3(x-60)2+1200,
∴顶点坐标为(60,1200);
当x=40时,W=-3(40-60)2+1200=0;
当x=70时,W=-3(70-60)2+1200=900;
图象为:
(4)由函数图象可以看出,当牛奶售价为60元时,平均每天的利润最大.最大利润为1200元.
当50<x≤70,y=90-3(x-50)=-3x+240,
∴平均每天销售量y(箱)与每箱售价x(元)之间的函数关系式为:y=-3x+240(40≤x≤70);
(2)W=(x-40)•y
=(x-40)(-3x+240)
=-3x2+360x-9600,
∴平均每天销售这种牛奶的利润W(元),与每箱牛奶的售价x(元)之间的二次函数关系式为W=-3x2+360x-9600(40≤x≤70);

(3)W=-3x2+360x-9600
=-3(x-60)2+1200,
∴顶点坐标为(60,1200);
当x=40时,W=-3(40-60)2+1200=0;
当x=70时,W=-3(70-60)2+1200=900;
图象为:
(4)由函数图象可以看出,当牛奶售价为60元时,平均每天的利润最大.最大利润为1200元.
点评:本题考查了二次函数的应用:先把二次函数关系式变形成顶点式:y=a(x-k)2+h,当a<0,x=k时,y有最大值h;当a>0,x=k时,y有最小值h.也考查了利润的含义.

练习册系列答案
相关题目
一个正数的算术平方根是a,那么比这个正数大2的数的算术平方根是( )
| A、a2+2 | ||
B、±
| ||
C、
| ||
D、
|
下列图形中不是中心对称图形的是( )
| A、等边三角形 | B、矩形 |
| C、菱形 | D、圆 |
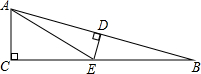 如图,在△ABC中,∠C=90°,∠B=15°,D是AB的中点,DE⊥AB于D,交BC于E,则∠CAE的度数是( )
如图,在△ABC中,∠C=90°,∠B=15°,D是AB的中点,DE⊥AB于D,交BC于E,则∠CAE的度数是( )| A、15° | B、30° |
| C、60° | D、75° |
若点P(1-m,2m-4)在第四象限内,则m的取值范围是( )
| A、m<1 | B、1<m<2 |
| C、m<2 | D、m>2 |
 如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,
如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,