题目内容
如图，在△ABC中，∠ACB=90°，CD是斜边上的高线，CE平分∠ACB，且∠B=30°，求∠DCE的度数．考点：三角形内角和定理
专题：
分析：在△BCD中可求得∠BCD，再由角平分线可求得∠BCE，利用角的和差可求得∠DCE．
解答：解：
∵CD是斜边上的高线，
∴∠BCD=90°-∠B=90°-30°=60°，
∵CE平分∠ACB，
∴∠BCE=
∠ACB=45°，
∴∠DCE=∠BCD-∠BCE=60°-45°=15°．
∵CD是斜边上的高线，
∴∠BCD=90°-∠B=90°-30°=60°，
∵CE平分∠ACB，
∴∠BCE=
| 1 |
| 2 |
∴∠DCE=∠BCD-∠BCE=60°-45°=15°．
点评：本题主要考查三角形内角和定理及角平分线的定义，掌握三角形内角和为180°是解题的关键．
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
下列代数式的值中，一定是正数的是（ ）
| A、（x+1）2 |
| B、|x+1|+2 |
| C、（-x）2 |
| D、-x2+1 |
尺规作图：（保留作图痕迹，不写作法）已知：如图，线段m，n，∠α．求作：△ABC，使得∠A=∠α，AB=m，AC=n．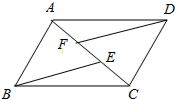
如图，AD=BC，AE=CF，DF=BE，找出图中一对全等的三角形，并说明理由．
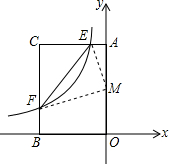如图，在平面直角坐标系xOy中，矩形AOBC的AO边在y轴上，BO边在x轴上，C点坐标为（-2，3），反比例函数y=