题目内容
 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求:AF、BD、CF的长.
如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求:AF、BD、CF的长.考点:三角形的内切圆与内心
专题:
分析:首先根据切线的性质定理求出AF的长;然后借助余弦定理求出∠A的余弦值;再次利用余弦定理求出线段CF的长度问题即可解决.
解答: 解:∵⊙O是△ABC的内切圆,
解:∵⊙O是△ABC的内切圆,
∴AE=AF(设为x),BD=BF(设为y),CD=CE(设为z),
又∵AB=13cm,BC=14cm,CA=9cm,
∴
,
由①+②+③得:2(x+y+z)=36,
∴x+y+z=18④,
由④-①得z=5;由④-②得x=4;由④-③得y=9;
∴AF=4,AC=9;
∵cosA=
=
=
;
∴CF=
=
=
=
=
.
 解:∵⊙O是△ABC的内切圆,
解:∵⊙O是△ABC的内切圆,∴AE=AF(设为x),BD=BF(设为y),CD=CE(设为z),
又∵AB=13cm,BC=14cm,CA=9cm,
∴
|
由①+②+③得:2(x+y+z)=36,
∴x+y+z=18④,
由④-①得z=5;由④-②得x=4;由④-③得y=9;
∴AF=4,AC=9;
∵cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
| 132+92-142 |
| 2×13×9 |
=
| 3 |
| 13 |
∴CF=
| AF2+AC2-2AF•AC•cosA |
=
42+92-2×4×9×
|
=
16+81-
|
=
|
=
| ||
| 13 |
点评:该命题主要考查了三角形的内切圆及其性质的应用问题;解题的关键是灵活运用切线的性质求出有关线段长;借助余弦定理分析、判断、求解或证明.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列说法中,你认为正确的是( )
| A、单项式-3x2y的次数是2 |
| B、等边三角形是中心对称图形 |
| C、任意多边形的外角和是360° |
| D、矩形对角线互相垂直 |
 尺规作图:(保留作图痕迹,不写作法)已知:如图,线段m,n,∠α.求作:△ABC,使得∠A=∠α,AB=m,AC=n.
尺规作图:(保留作图痕迹,不写作法)已知:如图,线段m,n,∠α.求作:△ABC,使得∠A=∠α,AB=m,AC=n.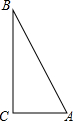 如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.
如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.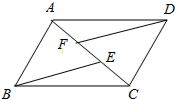 如图,AD=BC,AE=CF,DF=BE,找出图中一对全等的三角形,并说明理由.
如图,AD=BC,AE=CF,DF=BE,找出图中一对全等的三角形,并说明理由.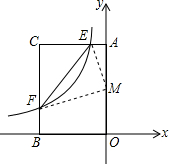 如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=
如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=