题目内容
16. 如图,在⊙O中,直径AB与弦CD相交于点E,已知AE=10,BE=2,∠AEC=45°,则弦CD的长是4$\sqrt{7}$.
如图,在⊙O中,直径AB与弦CD相交于点E,已知AE=10,BE=2,∠AEC=45°,则弦CD的长是4$\sqrt{7}$.
分析 如图,作辅助线;首先求出OC的长;借助勾股定理求出OF的长;再次借助勾股定理求出CF的长,即可解决问题.
解答 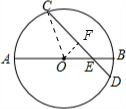 解:如图,连接OC,过点O作OF⊥CD于点F;
解:如图,连接OC,过点O作OF⊥CD于点F;
∵AE=10,BE=2,
∴OC=OA=6,OE=6-2=4;
∵∠AEC=45°,
∴∠EOF=90°-45°=45°,
∴∠OEF=∠EOF=45°,
∴OF=EF(设为λ);
由勾股定理得:λ2+λ2=42;
解得:λ=2$\sqrt{2}$;
由勾股定理得:CF2=OC2-OF2,
解得:CF=2$\sqrt{7}$,
∴CD=2CF=4$\sqrt{7}$,
故答案为4$\sqrt{7}$.
点评 该题主要考查了垂径定理、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,构造直角三角形;解题的关键是灵活运用垂径垂径定理、勾股定理等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
4.某商品经过两次降价,零售价降为原来的$\frac{1}{2}$,已知两次降价的百分率均为x,则列出方程正确的是( )
| A. | ${(1+x)^2}=\frac{1}{2}$ | B. | ${(1-x)^2}=\frac{1}{2}$ | C. | (1+x)2=2 | D. | (1-x)2=2 |
11.数据0,1,1,3,3,4的中位数和平均数分别是( )
| A. | 2和2 | B. | 2和2.4 | C. | 1和2 | D. | 3和2 |
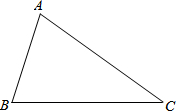 如图,已知△ABC,按要求画图、填空:
如图,已知△ABC,按要求画图、填空: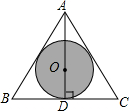 如图,已知⊙O是等边三角形ABC纸板的内切圆,并给⊙O涂上黑色,将这块三角形纸板作为靶子,玩飞镖游戏(设每次飞镖均能落在三角形纸板内,且落在任意一点的机会都相同).问:飞镖落在黑色区域的概率大,还是落在白色区域大?为什么?
如图,已知⊙O是等边三角形ABC纸板的内切圆,并给⊙O涂上黑色,将这块三角形纸板作为靶子,玩飞镖游戏(设每次飞镖均能落在三角形纸板内,且落在任意一点的机会都相同).问:飞镖落在黑色区域的概率大,还是落在白色区域大?为什么?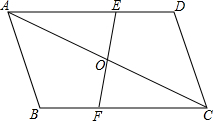 如图,在?ABCD中,过AC中点O作直线分别交AD、BC于点E、F.求证:OE=OF.
如图,在?ABCD中,过AC中点O作直线分别交AD、BC于点E、F.求证:OE=OF.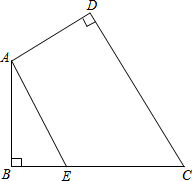 如图,四边形ABCD中,∠D=∠B=90°,∠AEC=∠BAD,求证:AE∥DC.
如图,四边形ABCD中,∠D=∠B=90°,∠AEC=∠BAD,求证:AE∥DC.