题目内容
2.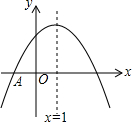 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据抛物线开口向下判断出a<0,再根据顶点横坐标用a表示出b,根据与y轴的交点求出c的取值范围,然后判断出①错误,②正确,根据点A的坐标用c表示出a,再根据c的取值范围解不等式求出③正确,根据顶点坐标判断出④正确,⑤错误,从而得解.
解答 解:∵抛物线开口向下,
∴a<0,
∵顶点坐标(1,n),
∴对称轴为直线x=1,
∴-$\frac{b}{2a}$=1,
∴b=-2a>0,
∵与y轴的交点在(0,3),(0,4)之间(包含端点),
∴3≤c≤4,
∴abc<0,故①错误,
3a+b=3a+(-2a)=a<0,故②正确,
∵与x轴交于点A(-1,0),
∴a-b+c=0,
∴a-(-2a)+c=0,
∴c=-3a,
∴3≤-3a≤4,
∴-$\frac{4}{3}$≤a≤-1,故③正确,
∵顶点坐标为(1,n),
∴当x=1时,函数有最大值n,
∴a+b+c≥am2+bm+c,
∴a+b≥am2+bm,故④正确,
一元二次方程ax2+bx+c=n有两个相等的实数根x1=x2=1,故⑤错误,
综上所述,结论正确的是②③④共3个.
故选B.
点评 本题考查了抛物线与x轴的交点,二次函数的性质,主要利用了二次函数的开口方向,对称轴,最值问题,以及二次函数图象上点的坐标特征,关键在于根据顶点横坐标表示出a、b的关系.

练习册系列答案
相关题目
13. 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | $\frac{π}{6}$ | C. | 4$\sqrt{3}$-$\frac{2π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |
7.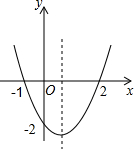 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )
二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )
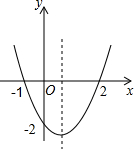 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )
二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
14.下列式子成立的是( )
| A. | 3a+4a=7a | B. | -7x2+5x2=-2 | C. | 2a2b-2b2a=0 | D. | 3a+4b=7ab |
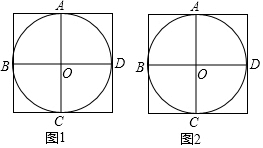 在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.
在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.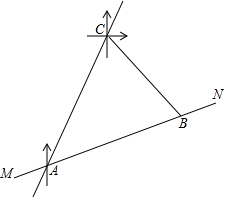 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)