题目内容
10.先化简,再求代数式$\frac{{b}^{2}-{a}^{2}}{{a}^{2}-ab}$÷(a+$\frac{2ab+{b}^{2}}{a}$)•($\frac{1}{a}$+$\frac{1}{b}$)的值,其中a=2sin45°+tan60°,b=$\sqrt{2}$-2cos30°.分析 先把括号内通分,再把除法运算化为乘法运算和分子分母因式分解,接着约分得到原式=-$\frac{1}{ab}$,然后根据特殊角的三角函数值计算出a和b的值,再把a、b的值代入计算即可.
解答 解:原式=-$\frac{(a-b)(a+b)}{a(a-b)}$÷$\frac{{a}^{2}+2ab+{b}^{2}}{a}$•$\frac{a+b}{ab}$
=-$\frac{(a-b)(a+b)}{a(a-b)}$•$\frac{a}{(a+b)^{2}}$•$\frac{a+b}{ab}$
=-$\frac{1}{ab}$,
当a=2×$\frac{\sqrt{2}}{2}$+$\sqrt{3}$=$\sqrt{2}$+$\sqrt{3}$,b=$\sqrt{2}$-2×$\frac{\sqrt{3}}{2}$=$\sqrt{2}$-$\sqrt{3}$,原式=-$\frac{1}{(\sqrt{2}+\sqrt{3})(\sqrt{2}-\sqrt{3})}$=1.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了特殊角的三角函数值.

练习册系列答案
相关题目
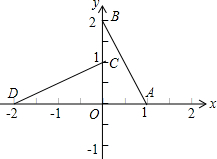 如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A(1,0),与y轴交于点B(0,2).
如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A(1,0),与y轴交于点B(0,2).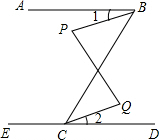 如图,已知∠ABC与∠ECB互补,∠1=∠2,∠P与∠Q一定相等吗?说说你的理由.
如图,已知∠ABC与∠ECB互补,∠1=∠2,∠P与∠Q一定相等吗?说说你的理由.