题目内容
3.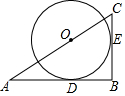 如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为$\frac{6}{5}$.
如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为$\frac{6}{5}$.
分析 连接OE、OD,根据切线的性质得出∠OEC=∠ODA=90°,∠ODB=∠OEB=90°,求出四边形OEBD是正方形,根据正方形的性质得出OE=OD=BE=BD,根据相似三角形的判定得出△OEC∽△ADO,得出比例式,代入求出即可.
解答 解:
连接OE、OD,
∵⊙O与AB、BC分别切于点D、E,∠B=90°,
∴∠OEC=∠ODA=90°,∠ODB=∠B=∠OEB=90°,
∵OD=OE,
∴四边形OEBD是正方形,
∴OE=OD=DB=BE,
设OE=OD=DB=BE=R,
∵四边形OEBD是正方形,
∴OE∥AB,
∴∠COE=∠A,
∵∠OEC=∠ODA=90°,
∴△OEC∽△ADO,
∴$\frac{AD}{OD}$=$\frac{OE}{CE}$,
∴$\frac{3-R}{R}$=$\frac{R}{2-R}$,
解得:R=$\frac{6}{5}$,
故答案为:$\frac{6}{5}$.
点评 本题考查了正方形的性质和判定,切线的性质,相似三角形的性质和判定等知识点,能求出△OEC∽△ADO是解此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13.分式方程$\frac{x}{x-1}$-$\frac{2}{x}$=1的解为( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=2或 x=3 |
 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为10°.
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为10°. 如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.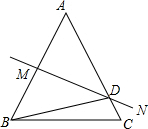 如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为14cm.
如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为14cm.