题目内容
8．
如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB的度数为10°．
分析 根据直角三角形两锐角互余求出∠B，根据翻折变换的性质可得∠CA′D=∠A，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
解答 解：∵∠ACB=90°，∠A=50°，
∴∠B=90°-50°=40°，
∵折叠后点A落在边CB上A′处，
∴∠CA′D=∠A=50°，
由三角形的外角性质得，∠A′DB=∠CA′D-∠B=50°-40°=10°．
故答案为：10°．
点评 本题考查了翻折变换，直角三角形两锐角互余，三角形的一个外角等于与它不相邻的两个内角的和的性质，翻折前后对应边相等，对应角相等．
练习册系列答案
相关题目
18．
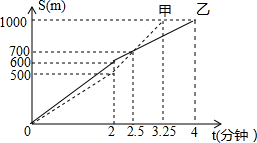甲乙两人在操场上赛跑，他们赛跑的路程s（m）与时间t（min）之间的函数关系如图所示，则下列说法错误的是（ ）
甲乙两人在操场上赛跑，他们赛跑的路程s（m）与时间t（min）之间的函数关系如图所示，则下列说法错误的是（ ）| A． | 甲乙两人在出发2.5 min时相遇 | |
| B． | 甲乙两人相遇时到起点的距离为700 m | |
| C． | 比赛到2min和3min时，甲乙两人都相距100 m | |
| D． | 比赛到2 min以后，甲超过乙 |
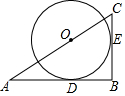如图，在△ABC中，∠B=90°，AB=3，BC=2，点O在AC边上，⊙O与AB、BC分别切于点D、E，则⊙O的半径长为$\frac{6}{5}$．
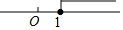学完一元一次不等式的解法后，老师布置了如下练习：