题目内容
已知在△ABC中,AB=AC=13,BC=10,点D、E分别是AB、AC的中点,那么以点D为圆心,DE为半径的圆与直线BC的位置关系是 .
考点:直线与圆的位置关系
专题:
分析:过点A作AF⊥BC于点F,根据勾股定理求出AF的长,再由点D、E分别是AB、AC的中点得出DE是△ABC的中位线,故可得出DE即GF的长,由此可得出结论.
解答: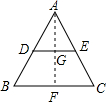 解:过点A作AF⊥BC于点F,
解:过点A作AF⊥BC于点F,
∵AB=AC=13,BC=10,
∴BF=
BC=5,
∴AF=
=
=12.
∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=
BC=5,GF=
AF=6,
∵5<6,
∴⊙D与直线BC的位置关系是相离.
故答案为:相离.
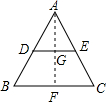 解:过点A作AF⊥BC于点F,
解:过点A作AF⊥BC于点F,∵AB=AC=13,BC=10,
∴BF=
| 1 |
| 2 |
∴AF=
| AB2-BF2 |
| 132-52 |
∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∵5<6,
∴⊙D与直线BC的位置关系是相离.
故答案为:相离.
点评:考查了等腰三角形的性质和勾股定理,三角形的面积,解题的关键是得到点D到直线AC的距离.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 两个一次函数的图象如图,
两个一次函数的图象如图,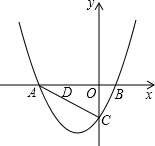 已知二次函数y=
已知二次函数y=