题目内容
5.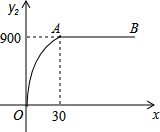 成都地铁规划到2020年将通车13条线路,近几年正是成都地铁加紧建设和密集开通的几年,市场对建材的需求量有所提高,根据市场调查分析可预测:投资水泥生产销售后所获得的利润y1(万元)与投资资金量x(万元)满足正比例关系y1=20x;投资钢材生产销售的后所获得的利润y2(万元)与投资资金量x(万元)满足函数关系的图象如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).
成都地铁规划到2020年将通车13条线路,近几年正是成都地铁加紧建设和密集开通的几年,市场对建材的需求量有所提高,根据市场调查分析可预测:投资水泥生产销售后所获得的利润y1(万元)与投资资金量x(万元)满足正比例关系y1=20x;投资钢材生产销售的后所获得的利润y2(万元)与投资资金量x(万元)满足函数关系的图象如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).(1)直接写出当0<x<30及x>30时,y2与x之间的函数关系式;
(2)某建材经销公司计划投资100万元用于生产销售水泥和钢材两种材料,若设投资钢材部分的资金量为t(万元),生长销售完这两种材料后获得的总利润为W(万元).
①求W与t之间的函数关系式;
②若要求投资钢材部分的资金量不得少于45万元,那么当投资钢材部分的资金量为多少万元时,获得的总利润最大?最大总利润是多少?
分析 (1)当0<x≤30时,根据顶点A的坐标设其顶点式,将原点代入可得其解析式,当x>30时,可得y2=900;
(2)①设投资钢材部分的资金量为t万元,则投资生产水泥的资金量为(100-t)万元,分0<t≤30、t>30两种情况,根据W=y1+y2可得函数关系式;
②由t≥45可知W=-20t+2900,根据一次函数性质可得最值情况.
解答 解:(1)当0<x≤30时,根据题意设y2=a(x-30)2+900,
将原点(0,0)代入,得:900a+900=0,解得:a=-1,
∴y2=-(x-30)2+900=-x2+60x,
当x>30时,y2=900;
(2)①设投资钢材部分的资金量为t万元,则投资生产水泥的资金量为(100-t)万元,
当0<t≤30时,W=y1+y2=20(100-t)+(-t2+60t)=-t2+40t+2000,
当t>30时,W=20(100-t)+900=-20t+2900;
②∵t≥45,
∴W=-20t+2900,W随t的增大而减小,
∴当t=45时,W最大值=2000万元
答:当投资钢材部分的资金量为45万元时,获得的总利润最大,最大总利润是2000万元.
点评 本题主要考查待定系数法求二次函数解析式及二次函数的实际应用,根据投资量的不同分情况确定其函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.二次函数y=x2+4x+7的最小值是( )
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
10.某校参加校园青春健身操比赛的16名运动员的身高如表:
则该校16名运动员身高的平均数和中位数分别是(单位:cm)( )
| 身高(cm) | 172 | 173 | 175 | 176 |
| 人数(个) | 4 | 4 | 4 | 4 |
| A. | 173cm,173cm | B. | 174cm,174cm | C. | 173cm,174cm | D. | 174cm,175cm |
15.若a<b,则下列不等式成立的是( )
| A. | -a>-b | B. | -a+1>b+1 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac<bc |
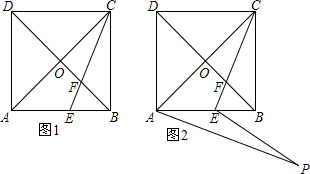
 如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).
如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).
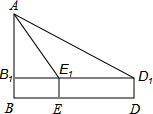 在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)
在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)